如图,在 $\Delta ABC$ 中,$AB=AC$,$D$ 是边 $BC$ 的中点,$E$ 是 $\Delta ABC$ 外一点,满足 $CE\bot AB$,$BE=BD$ 。过线段 $BE$ 的中点 $M$ 作直线 $MF\bot BE$,交 $\Delta ABD$ 的外接圆的劣弧 $AD$ 于点 $F$ 。求证:$ED\bot DF$ 。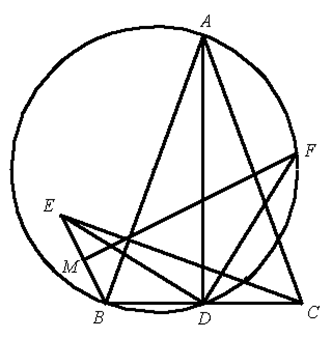

【难度】
【出处】
2010第9届CGMO试题
【标注】
【答案】
略
【解析】
如图,易知 $AD\bot BC$ 。由此可知 $\Delta ABD$ 的外接圆圆心为线段 $AB$ 的中点 $O$ 。 延长 $FM$ 交 $\odot O$ 于点 $L$,联结 $OE$,过点 $O$ 作 $OH\bot FL$,$OK\bot AD$,分别交 $FL$、$AD$ 于点 $H$、$K$ 。设直线 $FM$ 分别与直线 $ED$、$AB$、$AD$ 交于点 $S$、$I$、$P$,直线 $CE$ 与 $AB$ 交于点 $N$ 。由条件知 $CN\bot AB$ 。所以,$A$、$N$、$D$、$C$ 四点共圆。故 $BD\cdot BC=BN\cdot AB$ 。因为 $BC=2BE$,$AB=2BO$,所以 $B{{E}^{2}}=BN\cdot BO$ 。由射影定理得 $OE\bot BE$ 。从而,四边形 $OEMH$ 是矩形。则 $OH=EM=\frac{1}{2}BE$ 。因为 $O$ 是 $AB$ 的中点,且 $OK\parallel BD$,所以 $OK=\frac{1}{2}BD=\frac{1}{2}BE=OH$ 。于是 $FL=AD$ 。从而弧 $LD=$ 弧 $AF$,故 $\angle PFD=\angle PDF$ 。因为 $MF\bot BE$,所以 $\angle BED+\angle MSE={{90}^{{}^\circ }}$ 。而 $\angle PDS+\angle BDE={{90}^{{}^\circ }}$,且 $\angle BED=\angle BDE$,于是 $\angle PDS=\angle MSE=\angle DSP$ 。因此,$\angle FDS={{90}^{{}^\circ }}$ 即 $ED\bot FD$ 。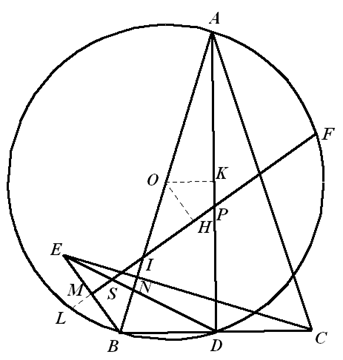

答案
解析
备注