如图,在锐角 $\Delta ABC$ 中,$AB$ > $AC$,$M$ 是边 $BC$ 的中点,$\angle BAC$ 的外角平分线交直线 $BC$ 于点 $P$ 。点 $K$、$F$ 在直线 $PA$ 上,使得 $MF\bot BC$,$MK\bot PA$ 。求证:$B{{C}^{2}}=4PF\cdot AK$ 。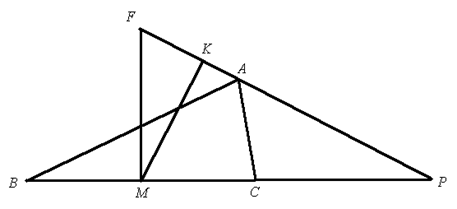

【难度】
【出处】
2010第9届CGMO试题
【标注】
【答案】
略
【解析】
如图,设 $\Delta ABC$ 的外接圆 $\odot O$ 交直线 $FM$ 于点 $D$,$AD$ 交 $BC$ 于点 $E$ 。易知 $AD$ 平分 $\angle BAC$ 。所以 $AD\bot AP$,$AD\parallel MK$ 。故 $\frac{MD}{FM}=\frac{AK}{FK}$ 。因为 $\angle FMC=\angle FAD={{90}^{{}^\circ }}$,所以 $F$、$M$、$E$、$A$ 四点共圆,有 $\angle AFD=\angle AEC=\angle ABC+\frac{1}{2}\angle BAC$ 。又 $\angle ABD=\angle ABC+\angle CBD=\angle ABC+\frac{1}{2}\angle BAC=\angle AFD$,则 $A$、$F$、$B$、$D$ 四点共圆。故 $A$、$F$、$B$、$D$、$C$ 五点共圆。根据圆幂定理得 $PA\cdot PF=PC\cdot PB=\left( PM-MC \right)\left( PM+BM \right)=P{{M}^{2}}-B{{M}^{2}}$(1)。对 $Rt\Delta FMP$ 利用射影定理得($P{{M}^{2}}=PK\cdot PF$)。(2)-(1)得 $B{{M}^{2}}=PK\cdot PF-PA\cdot PF=PF\left( PK-PA \right)=PF\cdot AK$ 。因为 $B{{M}^{2}}={{\left(\frac{BC}{2} \right)}^{2}}=\frac{B{{C}^{2}}}{4}$,所以结论成立。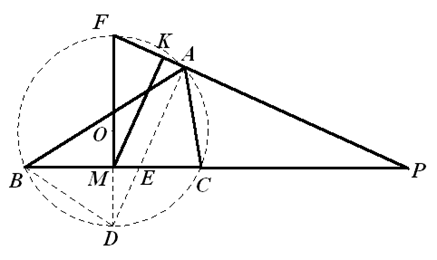

答案
解析
备注