如图,四边形 $ABCD$ 的对角线 $AC$ 与 $BD$ 交于点 $E$,边 $AB$、$CD$ 的中垂线交于点 $F$,$M$、$N$ 分别为边 $AB$、$CD$ 的中点,直线 $EF$ 分别与边 $BC$、$AD$ 交于点 $P$、$Q$ 。若 $MF\cdot CD=NF\cdot AB$,$DQ\cdot BP=AQ\cdot CP$,证明:$PQ\bot BC$ 。

【难度】
【出处】
2011第10届CGMO试题
【标注】
【答案】
略
【解析】
如图,联结 $AF$、$BF$、$CF$、$DF$ 。由题设知,$\vartriangle AFB$、$\vartriangle CFD$ 都是等腰三角形,
$FM$、$FN$ 分别为这两个等腰三角形底边上的高。
由 $MF\cdot CD=NF\cdot AB$,知 $\vartriangle AFB\sim \vartriangle DFC\Rightarrow \angle AFB=\angle CFD,\angle FAB=\angle FDC$ 。
由 $\angle AFB=\angle CFD$,得 $\angle BFD=\angle CFA$ 。因为 $FB=FA$,$FD=FC$
所以 $\vartriangle BFD\cong \vartriangle AFC\Rightarrow \angle FAC=\angle FBD,\angle FCA=\angle FDB$ 。
从而 $A$、$B$、$F$、$E$,$C$、$D$、$E$、$F$ 分别四点共圆。
故 $\angle FEB=\angle FAB=\angle FDC=\angle FEC\Rightarrow $ 直线 $EP$ 是 $\angle BEC$ 的角平分线 $\Rightarrow \frac{EB}{EC}=\frac{BP}{CP}$ 。
同理,$\frac{ED}{EA}=\frac{QD}{AQ}$ 。由 $DQ\cdot BP=AQ\cdot CP$,得 $EB\cdot ED=EC\cdot EA$ 。
由此知四边形 $ABCD$ 为圆内接四边形,且 $F$ 为其外接圆的圆心。
因 $\angle EBC=\frac{1}{2}\angle DFC=\frac{1}{2}\angle AFB=\angle ECB$,所以,$EP\bot BC$ 。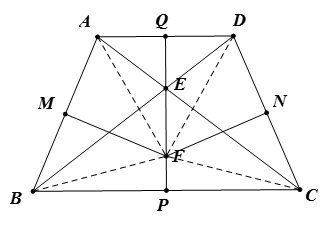
$FM$、$FN$ 分别为这两个等腰三角形底边上的高。
由 $MF\cdot CD=NF\cdot AB$,知 $\vartriangle AFB\sim \vartriangle DFC\Rightarrow \angle AFB=\angle CFD,\angle FAB=\angle FDC$ 。
由 $\angle AFB=\angle CFD$,得 $\angle BFD=\angle CFA$ 。因为 $FB=FA$,$FD=FC$
所以 $\vartriangle BFD\cong \vartriangle AFC\Rightarrow \angle FAC=\angle FBD,\angle FCA=\angle FDB$ 。
从而 $A$、$B$、$F$、$E$,$C$、$D$、$E$、$F$ 分别四点共圆。
故 $\angle FEB=\angle FAB=\angle FDC=\angle FEC\Rightarrow $ 直线 $EP$ 是 $\angle BEC$ 的角平分线 $\Rightarrow \frac{EB}{EC}=\frac{BP}{CP}$ 。
同理,$\frac{ED}{EA}=\frac{QD}{AQ}$ 。由 $DQ\cdot BP=AQ\cdot CP$,得 $EB\cdot ED=EC\cdot EA$ 。
由此知四边形 $ABCD$ 为圆内接四边形,且 $F$ 为其外接圆的圆心。
因 $\angle EBC=\frac{1}{2}\angle DFC=\frac{1}{2}\angle AFB=\angle ECB$,所以,$EP\bot BC$ 。

答案
解析
备注