给定非负实数 $\alpha $ 。求最小实数 $\lambda =\lambda (\alpha )$,使得对任意复数 ${{z}_{1}}$、${{z}_{2}}$ 和实数 $x\in [0,1]$,若 $\left| {{z}_{1}} \right|\leqslant \alpha \left| {{z}_{1}}-{{z}_{2}} \right|$,则 $\left| {{z}_{1}}-x{{z}_{2}} \right|\leqslant \lambda \left| {{z}_{1}}-{{z}_{2}} \right|$ 。
【难度】
【出处】
2011第10届CGMO试题
【标注】
【答案】
略
【解析】
如图,在复平面内,点 $A$、$B$、$C$ 对应的复数分别为 ${{z}_{1}}$、${{z}_{2}}$、$x{{z}_{2}}$ 。显然,点 $C$ 在线段 $OB$ 上。向量 $BA$、$CA$ 分别对应的复数为 ${{z}_{1}}-{{z}_{2}}$、${{z}_{1}}-x{{z}_{2}}$ 。由 $\left| {{z}_{1}}\right|\leqslant \alpha \left| {{z}_{1}}-{{z}_{2}} \right|$,得 $\left| \right|\leqslant \alpha \left| \right|$ 。
故 ${{\left| {{z}_{1}}-x{{z}_{2}} \right|}_{\max}}={{\left| \right|}_{\max }}=\max\{\left| \right|,\left| \right|\}=\max \{\left| {{z}_{1}}\right|,\left| {{z}_{1}}-{{z}_{2}} \right|\}=\max \{\alpha \left|{{z}_{1}}-{{z}_{2}} \right|,\left| {{z}_{1}}-{{z}_{2}} \right|\}$
于是,$\lambda (\alpha )=\max \{\alpha ,1\}$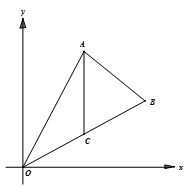
故 ${{\left| {{z}_{1}}-x{{z}_{2}} \right|}_{\max}}={{\left| \right|}_{\max }}=\max\{\left| \right|,\left| \right|\}=\max \{\left| {{z}_{1}}\right|,\left| {{z}_{1}}-{{z}_{2}} \right|\}=\max \{\alpha \left|{{z}_{1}}-{{z}_{2}} \right|,\left| {{z}_{1}}-{{z}_{2}} \right|\}$
于是,$\lambda (\alpha )=\max \{\alpha ,1\}$

答案
解析
备注