如图，已知 $\odot O$ 为 $\vartriangle ABC$ 的边 $BC$ 上的旁切圆，点 $D$、$E$ 分别在线段 $AB$、$AC$ 上，使得 $DE\parallel BC$，$\odot {{O}_{1}}$ 为 $\vartriangle ADE$ 的内切圆，${{O}_{1}}B$ 与 $DO$、${{O}_{1}}C$ 与 $EO$ 分别交于点 $F$、$G$，$\odot O$ 与 $BC$ 切于点 $M$，$\odot {{O}_{1}}$ 与 $DE$ 切于点 $N$ 。证明：$MN$ 平分线段 $FG$ 。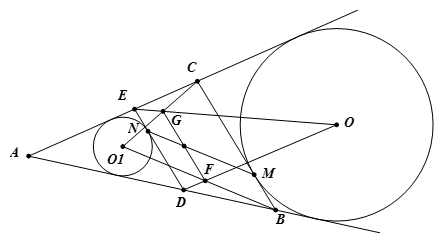
【难度】
【出处】
2011第10届CGMO试题
【标注】
【答案】
略
【解析】
若 $AB=AC$，则图形关于 $\angle BAC$ 的角平分线成轴对称，结论显然成立。下面不妨设 $AB>AC$ 。
如图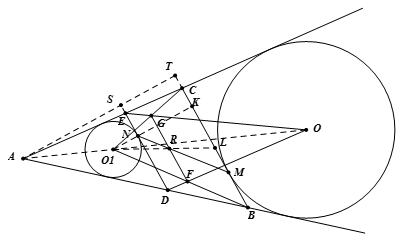
设线段 $BC$ 的中点为 $L$，联结 ${{O}_{1}}L$ 与线段 $FG$ 交于点 $R$ 。联结 ${{O}_{1}}N$ 并延长与直线 $BC$ 交于点 $K$，作 $AT\bot BC$ 于点 $T$，与直线 $DE$ 交于点 $S$，联结 $AO$ 。
显然，点 ${{O}_{1}}$ 在线段 $AO$ 上。
由梅涅劳斯定理得 $\frac{{{O}_{1}}F}{FB}\cdot \frac{BD}{DA}\cdot\frac{AO}{O{{O}_{1}}}=1$（1．4），$\frac{{{O}_{1}}G}{GC}\cdot \frac{CE}{EA}\cdot\frac{AO}{O{{O}_{1}}}=1$ 。
因为 $DE\parallel BC$，所以，$\frac{BD}{DA}=\frac{CE}{EA}$ 。因此，$\frac{{{O}_{1}}F}{FB}=\frac{{{O}_{1}}G}{GC}$，即 $FG\parallel BC$，故 $\frac{FR}{GR}=\frac{BL}{CL}=1$ 。
从而，$R$ 是 $FG$ 的中点。其次只需证明：$M$、$R$、$N$ 三点共线。
由梅涅劳斯定理的逆定理只需证明 $\frac{{{O}_{1}}R}{RL}\cdot\frac{LM}{MK}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．5）
由 $FR\parallel BL$ 及式（1．4）有 $\frac{{{O}_{1}}R}{RL}=\frac{{{O}_{1}}F}{FB}=\frac{O{{O}_{1}}}{AO}\cdot\frac{AD}{DB}$ 。
故式（1．5）等价于 $\frac{OO}{AO}\cdot\frac{AD}{DB}\cdot \frac{LM}{MK}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．6）
由于 ${{O}_{1}}K\bot DE$，$OM\bot BC$，$AT\bot BC$，$DE\parallel BC$，故 ${{O}_{1}}K$、$OM$、$AT$ 三条直线彼此平行。
由平行线分线段成比例，$\frac{O{{O}_{1}}}{AO}=\frac{MK}{MT}$ 。则式（1．6）$\Leftrightarrow \frac{AD}{DB}\cdot\frac{LM}{MT}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．7）
由于 $DE\parallel BC$，$KN\bot DE$，$ST\bot BC$，故四边形 $KNST$ 为矩形，因此 $KN=ST$ 。
再由 $DS\parallel BT$，得 $\frac{AD}{DB}=\frac{AS}{ST}$ 。则式（1．7）$\Leftrightarrow\frac{LM}{MT}=\frac{N{{O}_{1}}}{AS}$（1．8）
记 $BC=a$，$AC=b$，$AB=c$，则 $BM=\frac{a+b-c}{2}$，$BL=\frac{a}{2}$，$BT=c\cos \angle ABC=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a}$ 。
故 $\frac{LM}{MT}=\frac{BL-BM}{BT-BM}=\frac{\frac{c-b}{2}}{\frac{{{c}^{2}}-{{b}^{2}}+a(c-b)}{2a}}=\frac{a}{a+b+c}$
又因为 $\frac{N{{O}_{1}}}{AS}=\frac{\frac{2S\vartriangle ADE}{AD+DE+AE}}{\frac{2S\vartriangle ADE}{DE}}=\frac{DE}{AD+DE+AE}=\frac{a}{a+b+c}$，故式（1．8）成立。
如图
设线段 $BC$ 的中点为 $L$，联结 ${{O}_{1}}L$ 与线段 $FG$ 交于点 $R$ 。联结 ${{O}_{1}}N$ 并延长与直线 $BC$ 交于点 $K$，作 $AT\bot BC$ 于点 $T$，与直线 $DE$ 交于点 $S$，联结 $AO$ 。显然，点 ${{O}_{1}}$ 在线段 $AO$ 上。
由梅涅劳斯定理得 $\frac{{{O}_{1}}F}{FB}\cdot \frac{BD}{DA}\cdot\frac{AO}{O{{O}_{1}}}=1$（1．4），$\frac{{{O}_{1}}G}{GC}\cdot \frac{CE}{EA}\cdot\frac{AO}{O{{O}_{1}}}=1$ 。
因为 $DE\parallel BC$，所以，$\frac{BD}{DA}=\frac{CE}{EA}$ 。因此，$\frac{{{O}_{1}}F}{FB}=\frac{{{O}_{1}}G}{GC}$，即 $FG\parallel BC$，故 $\frac{FR}{GR}=\frac{BL}{CL}=1$ 。
从而，$R$ 是 $FG$ 的中点。其次只需证明：$M$、$R$、$N$ 三点共线。
由梅涅劳斯定理的逆定理只需证明 $\frac{{{O}_{1}}R}{RL}\cdot\frac{LM}{MK}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．5）
由 $FR\parallel BL$ 及式（1．4）有 $\frac{{{O}_{1}}R}{RL}=\frac{{{O}_{1}}F}{FB}=\frac{O{{O}_{1}}}{AO}\cdot\frac{AD}{DB}$ 。
故式（1．5）等价于 $\frac{OO}{AO}\cdot\frac{AD}{DB}\cdot \frac{LM}{MK}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．6）
由于 ${{O}_{1}}K\bot DE$，$OM\bot BC$，$AT\bot BC$，$DE\parallel BC$，故 ${{O}_{1}}K$、$OM$、$AT$ 三条直线彼此平行。
由平行线分线段成比例，$\frac{O{{O}_{1}}}{AO}=\frac{MK}{MT}$ 。则式（1．6）$\Leftrightarrow \frac{AD}{DB}\cdot\frac{LM}{MT}\cdot \frac{KN}{N{{O}_{1}}}=1$（1．7）
由于 $DE\parallel BC$，$KN\bot DE$，$ST\bot BC$，故四边形 $KNST$ 为矩形，因此 $KN=ST$ 。
再由 $DS\parallel BT$，得 $\frac{AD}{DB}=\frac{AS}{ST}$ 。则式（1．7）$\Leftrightarrow\frac{LM}{MT}=\frac{N{{O}_{1}}}{AS}$（1．8）
记 $BC=a$，$AC=b$，$AB=c$，则 $BM=\frac{a+b-c}{2}$，$BL=\frac{a}{2}$，$BT=c\cos \angle ABC=\frac{{{a}^{2}}+{{c}^{2}}-{{b}^{2}}}{2a}$ 。
故 $\frac{LM}{MT}=\frac{BL-BM}{BT-BM}=\frac{\frac{c-b}{2}}{\frac{{{c}^{2}}-{{b}^{2}}+a(c-b)}{2a}}=\frac{a}{a+b+c}$
又因为 $\frac{N{{O}_{1}}}{AS}=\frac{\frac{2S\vartriangle ADE}{AD+DE+AE}}{\frac{2S\vartriangle ADE}{DE}}=\frac{DE}{AD+DE+AE}=\frac{a}{a+b+c}$，故式（1．8）成立。
答案
解析
备注
