圆 ${{\Gamma }_{1}}$ 和圆 ${{\Gamma }_{2}}$ 外切于点 $T$,点 $A$、$E$ 在圆 ${{\Gamma}_{1}}$ 上,$AB$ 切圆 ${{\Gamma }_{2}}$ 于点 $B$,$ED$ 切圆 ${{\Gamma}_{2}}$ 于点 $D$,直线 $BD$、$AE$ 交于点 $P$ 。
a)求证:$\frac{AB}{AT}=\frac{ED}{ET}$
b)求证:$\angle ATP+\angle ETP=180{}^\circ $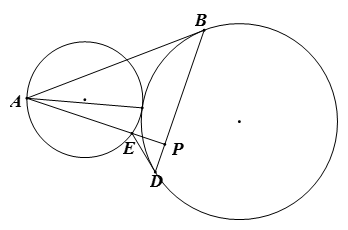
a)求证:$\frac{AB}{AT}=\frac{ED}{ET}$
b)求证:$\angle ATP+\angle ETP=180{}^\circ $

【难度】
【出处】
2012第11届CGMO试题
【标注】
【答案】
略
【解析】
延长 $AT$、$ET$ 于圆 ${{\Gamma }_{2}}$ 分别交于点 $H$、$G$,联结 $GH$ 。因为圆 ${{\Gamma }_{1}}$ 和圆 ${{\Gamma }_{2}}$ 关于点 $T$ 位似,$A$、$H$,$E$、$G$ 分别为对应点,则有 $\vartriangle ATE\sim \vartriangle HTG$,所以
$\frac{AT}{TH}=\frac{ET}{TG}\Rightarrow \frac{AH}{TH}=\frac{EG}{TG}$
由圆幂定理,得
$\frac{A{{B}^{2}}}{T{{H}^{2}}}=\frac{AT\cdot AH}{TH\cdot TH}=\frac{ET}{TG}\cdot \frac{EG}{TG}=\frac{E{{D}^{2}}}{T{{G}^{2}}}$
所以 $\frac{TH}{TG}=\frac{AB}{ED}$,故 $\frac{AT}{ET}=\frac{TH}{TG}=\frac{AB}{ED}$ 即有 $\frac{AB}{AT}=\frac{ED}{ET}$ 。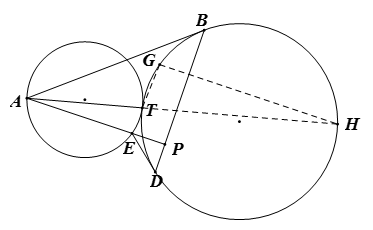
$\frac{AT}{TH}=\frac{ET}{TG}\Rightarrow \frac{AH}{TH}=\frac{EG}{TG}$
由圆幂定理,得
$\frac{A{{B}^{2}}}{T{{H}^{2}}}=\frac{AT\cdot AH}{TH\cdot TH}=\frac{ET}{TG}\cdot \frac{EG}{TG}=\frac{E{{D}^{2}}}{T{{G}^{2}}}$
所以 $\frac{TH}{TG}=\frac{AB}{ED}$,故 $\frac{AT}{ET}=\frac{TH}{TG}=\frac{AB}{ED}$ 即有 $\frac{AB}{AT}=\frac{ED}{ET}$ 。

答案
解析
备注