如图,$\odot {{O}_{1}}$ $\odot {{O}_{2}}$ 交于 $A$、$B$ 两点,延长 ${{O}_{1}}A$,与 $\odot {{O}_{2}}$ 交于点 $C$,延长 ${{O}_{2}}A$ 与 $\odot {{O}_{1}}$ 交于点 $D$,过点 $B$ 作 $BE$ // ${{O}_{2}}A$,与 $\odot {{O}_{1}}$ 交于另一点 $E$ 。若 $DE$ // ${{O}_{1}}A$,证明:$DC\bot C{{O}_{2}}$ 。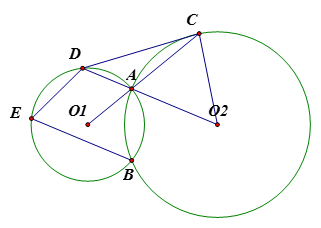

【难度】
【出处】
2014第13届CGMO试题
【标注】
【答案】
略
【解析】
由 $\angle {{O}_{1}}DA=\angle{{O}_{1}}AD=\angle {{O}_{2}}AC=\angle {{O}_{2}}CA$,知 ${{O}_{1}}$、${{O}_{2}}$、$C$、$D$ 四点共圆。故 $\angle D{{O}_{1}}{{O}_{2}}+\angle DC{{O}_{2}}=180{}^\circ $,因为 $BE$ // $AD$,所以 $AB=DE$ 。于是,$\angle ED{{O}_{1}}=\angle {{O}_{1}}AB$ 。又 $DE$ // ${{O}_{1}}A$,故 $\angle D{{O}_{1}}A=\angle ED{{O}_{1}}=\angle {{O}_{1}}AB$ 。从而,$D{{O}_{1}}$ // $AB$ 。而 $AB\bot{{O}_{1}}{{O}_{2}}$,则 $D{{O}_{1}}\bot {{O}_{1}}{{O}_{2}}$,即 $\angle D{{O}_{1}}{{O}_{2}}=90{}^\circ $ 。因此,$\angle DC{{O}_{2}}=90{}^\circ $,即 $DC\bot C{{O}_{2}}$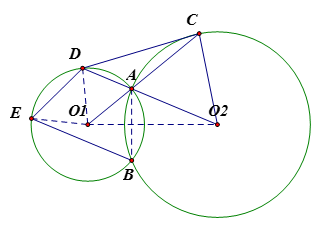

答案
解析
备注