如图，在锐角 $\vartriangle ABC$ 中，$AB>AC$，$D$、$E$ 分别为边 $AB$、$AC$ 的中点。 $\vartriangle ADE$ 的外接圆与 $\vartriangle BCE$ 的外接圆交于点 $P$（异于点 $E$），$\vartriangle ADE$ 的外接圆与的 $\vartriangle BCD$ 外接圆交于点 $Q$（异于点 $D$）。证明：$AP=AQ$ 。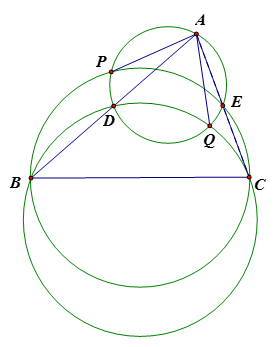
【难度】
【出处】
2014第13届CGMO试题
【标注】
【答案】
略
【解析】
如图，联结 $DE$、$PD$、$QE$、$PB$、$QC$、$PE$、$QD$ 。设 $QD$ 与 $AC$ 交于点 $R$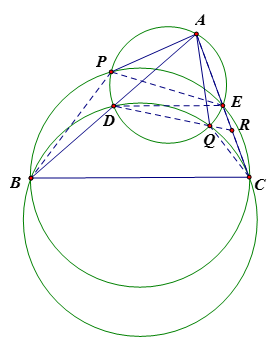
由圆周角定理得 $\angle APD=\pi -\angle AED=\pi -\angle ACB$，$\angle BPD=\angle BPE-\angle EPD=(\pi -\angle ACB)-\angle BAC=\angle ABC$，$\angle AQE=\angle ADE=\angle ABC$ $\angle CQE=\angle CQR+\angle RQE=\angle ABC+\angle DAE=\pi -\angle ACB$ $\angle APB=\angle APD+\angle BPD=\angle AQE+\angle CQE=\angle AQC$
故 $\angle APB=\angle APD+\angle BPD=\angle AQE+\angle CQE=\angle AQC$
另一方面，在 $\vartriangle APB$ 中
$\frac{AP}{BP}=\frac{AP}{AD}\cdot \frac{BD}{BP}=\frac{\sin\angle ADP}{\sin \angle APD}\cdot \frac{\sin \angle BPD}{\sin \angle BDP}=\frac{\sin \angle BPD}{\sin \angle APD}=\frac{\sin \angle ABC}{\sin (\pi-\angle ACB)}$
类似地，在 $\vartriangle CQA$ 中，$\frac{CQ}{AQ}=\frac{\sin\angle ABC}{\sin (\pi -\angle ACB)}$ 。
因此，$\frac{AP}{BP}=\frac{CQ}{AQ}$ 。
结合 $\angle APB=\angle AQC$，知 $\vartriangle APB\sim \vartriangle CQA$ 。由于 $D$、$E$ 分别为这两个相似三角形对应边的中点，故 $\vartriangle APD\sim\vartriangle CQE$ 。于是，$\angle ADP=\angle CEQ=\angle ADQ$ 。因此，$AP=AQ$ 。
由圆周角定理得 $\angle APD=\pi -\angle AED=\pi -\angle ACB$，$\angle BPD=\angle BPE-\angle EPD=(\pi -\angle ACB)-\angle BAC=\angle ABC$，$\angle AQE=\angle ADE=\angle ABC$ $\angle CQE=\angle CQR+\angle RQE=\angle ABC+\angle DAE=\pi -\angle ACB$ $\angle APB=\angle APD+\angle BPD=\angle AQE+\angle CQE=\angle AQC$故 $\angle APB=\angle APD+\angle BPD=\angle AQE+\angle CQE=\angle AQC$
另一方面，在 $\vartriangle APB$ 中
$\frac{AP}{BP}=\frac{AP}{AD}\cdot \frac{BD}{BP}=\frac{\sin\angle ADP}{\sin \angle APD}\cdot \frac{\sin \angle BPD}{\sin \angle BDP}=\frac{\sin \angle BPD}{\sin \angle APD}=\frac{\sin \angle ABC}{\sin (\pi-\angle ACB)}$
类似地，在 $\vartriangle CQA$ 中，$\frac{CQ}{AQ}=\frac{\sin\angle ABC}{\sin (\pi -\angle ACB)}$ 。
因此，$\frac{AP}{BP}=\frac{CQ}{AQ}$ 。
结合 $\angle APB=\angle AQC$，知 $\vartriangle APB\sim \vartriangle CQA$ 。由于 $D$、$E$ 分别为这两个相似三角形对应边的中点，故 $\vartriangle APD\sim\vartriangle CQE$ 。于是，$\angle ADP=\angle CEQ=\angle ADQ$ 。因此，$AP=AQ$ 。
答案
解析
备注
