如图,在锐角 $\vartriangle ABC$ 中,$AB>AC$,$O$ 为外心,$D$ 为边 $BC$ 的中点.
以 $AD$ 为直径作圆与边 $AB$、$AC$ 分别交于点 $E$、$F$.过 $D$ 作 $DM∥AO$ 交 $EF$ 于点 $M$.求证:$EM=MF$.
以 $AD$ 为直径作圆与边 $AB$、$AC$ 分别交于点 $E$、$F$.过 $D$ 作 $DM∥AO$ 交 $EF$ 于点 $M$.求证:$EM=MF$.

【难度】
【出处】
2015第14届CGMO试题
【标注】
【答案】
略
【解析】
如图1,连接 $DE$、$DF$,过 $O$ 作 $ON\bot AB$ 交 $AB$ 于点 $N$.由题意可知,$DE\bot AB$,$DF\bot AC$.因此,$ON$ ∥ $DE$.又因为 $DM$ ∥ $AO$,所以 $\angle EDM=\angle AON$.
因为 $O$ 为 $\vartriangle ABC$ 外心,所以 $\angle AON=\angle ACB$.从而 $\angle EDM=\angle ACB$.
同理可得,$\angle FDM=\angle ABC$.
在 $\vartriangle EDF$ 中,有
.$\frac{EM}{MF}=\frac{DE\cdot \sin\angle EDM}{DF\cdot \sin \angle FDM}=\frac{DE\cdot \sin \angle ACB}{DF\cdot\sin \angle ABC}=\frac{DB\cdot \sin \angle ABC\cdot \sin \angle ACB}{DC\cdot\sin \angle ACB\cdot \sin \angle ABC}=1$,
即EM = MF.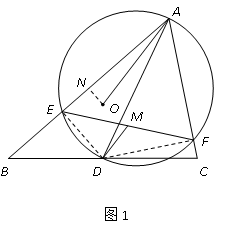
因为 $O$ 为 $\vartriangle ABC$ 外心,所以 $\angle AON=\angle ACB$.从而 $\angle EDM=\angle ACB$.
同理可得,$\angle FDM=\angle ABC$.
在 $\vartriangle EDF$ 中,有
.$\frac{EM}{MF}=\frac{DE\cdot \sin\angle EDM}{DF\cdot \sin \angle FDM}=\frac{DE\cdot \sin \angle ACB}{DF\cdot\sin \angle ABC}=\frac{DB\cdot \sin \angle ABC\cdot \sin \angle ACB}{DC\cdot\sin \angle ACB\cdot \sin \angle ABC}=1$,
即EM = MF.

答案
解析
备注