如图,两圆 ${{\Gamma }_{1}},{{\Gamma }_{2}}$ 外离,它们的一条外公切线与 ${{\Gamma }_{1}},{{\Gamma }_{2}}$ 分别切于点 $A,B$,一条内公切线与 ${{\Gamma }_{1}},{{\Gamma }_{2}}$ 分别切于点 $C,D$.设 $E$ 是直线 $AC,BD$ 的交点,$F$ 是 ${{\Gamma }_{1}}$ 上一点,过 $F$ 作
的切线与线段 $EF$ 的中垂线交于点 $M$,过 $M$ 作 $MG$ 切 ${{\Gamma}_{2}}$ 于点 $G$.求证:$MF=MG$.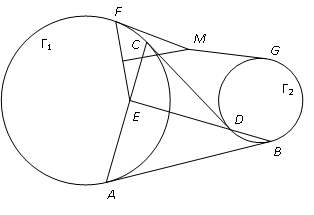
的切线与线段 $EF$ 的中垂线交于点 $M$,过 $M$ 作 $MG$ 切 ${{\Gamma}_{2}}$ 于点 $G$.求证:$MF=MG$.

【难度】
【出处】
2015第14届CGMO试题
【标注】
【答案】
略
【解析】
设 ${{\Gamma}_{1}},{{\Gamma }_{2}}$ 的圆心分别为 ${{O}_{1}},{{O}_{2}}$,直线 $AB,CD$ 交于点 $H$,连 $H{{O}_{1}},H{{O}_{2}}$.设 $J,K$ 分别是线段 $AB,CD$ 的中点,连 $JE,KE$.
由于 $HA,HC$ 是 ${{\Gamma }_{1}}$ 的切线,故 $H{{O}_{1}}$ 平分 $\angle AHC$,且 $AC\bot H{{O}_{1}}$.同理,$H{{O}_{2}}$ 平分 $\angle BHD$,且 $BD\bot H{{O}_{2}}$.由于 $H{{O}_{1}},H{{O}_{2}}$ 分别是 $\angle AHC$ 的内角平分线和外角平分线,故它们互相垂直,结合 $AC\bot H{{O}_{1}}$ 及 $BD\bot H{{O}_{2}}$ 知 $AC\bot BD$.
由于直角三角形斜边中线等于斜边一半,故 $JE=JA=JB,KE=KC=KD$.考虑 ${{\Gamma}_{1}},{{\Gamma }_{2}}$ 及以 $E$ 为圆心,0为半径的圆,由 $JE=JA=JB$ 知 $J$ 到这三个圆的幂相等,由 $KE=KC=KD$ 知 $K$ 到这三个圆的幂也相等.显然 $J,K$ 是两个不同的点,因此这三个圆必然有一条公共的根轴.由于 $M$ 在 $EF$ 的中垂线上,所以 $MF=ME$,结合 $MF$ 是 ${{\Gamma }_{1}}$ 的切线知 $M$ 在这三个圆的公共根轴上,又 $MG$ 是 ${{\Gamma }_{2}}$ 的切线,故 $MF=MG$,证毕.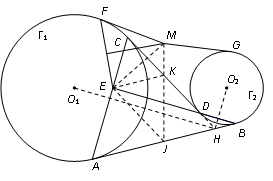
由于 $HA,HC$ 是 ${{\Gamma }_{1}}$ 的切线,故 $H{{O}_{1}}$ 平分 $\angle AHC$,且 $AC\bot H{{O}_{1}}$.同理,$H{{O}_{2}}$ 平分 $\angle BHD$,且 $BD\bot H{{O}_{2}}$.由于 $H{{O}_{1}},H{{O}_{2}}$ 分别是 $\angle AHC$ 的内角平分线和外角平分线,故它们互相垂直,结合 $AC\bot H{{O}_{1}}$ 及 $BD\bot H{{O}_{2}}$ 知 $AC\bot BD$.
由于直角三角形斜边中线等于斜边一半,故 $JE=JA=JB,KE=KC=KD$.考虑 ${{\Gamma}_{1}},{{\Gamma }_{2}}$ 及以 $E$ 为圆心,0为半径的圆,由 $JE=JA=JB$ 知 $J$ 到这三个圆的幂相等,由 $KE=KC=KD$ 知 $K$ 到这三个圆的幂也相等.显然 $J,K$ 是两个不同的点,因此这三个圆必然有一条公共的根轴.由于 $M$ 在 $EF$ 的中垂线上,所以 $MF=ME$,结合 $MF$ 是 ${{\Gamma }_{1}}$ 的切线知 $M$ 在这三个圆的公共根轴上,又 $MG$ 是 ${{\Gamma }_{2}}$ 的切线,故 $MF=MG$,证毕.

答案
解析
备注