如图所示,已知四边形 $ABCD$,$\angle BAD=90^{\circ}$,$\angle BCD=30^{\circ}$,$AB=AD$.$BC+CD=12\sqrt{3}$,连结 $AC$,线段 $AC$ 的长是否存在最小值,若存在,求出最小值;若不存在,请说明理由.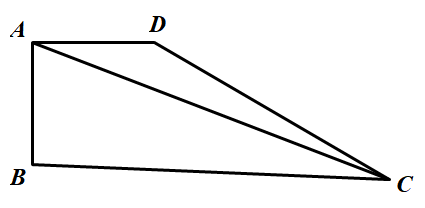

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
如图所示,将 $\triangle ABC$ 绕着 $A$ 旋转至 $\triangle ADC^{\prime}$,容易得到 $\triangle ACC^{\prime}$ 为等腰直角三角形,$CC^{\prime}=\sqrt{2}AC$,
在 $\triangle CDC^{\prime}$ 中,$\angle CDC^{\prime}=120^{\circ}$,设 $DC^{\prime}=BC=a$,$DC=b$,$a+b=12\sqrt{3}$
则 $C^{\prime}C^2=a^2+b^2+ab=(a+b)^2-ab\geqslant \dfrac{3}{4}(a+b)^2=324$,
故 $CC^{\prime}\geqslant 18$
$AC$ 的最小值为 $9\sqrt{2}$.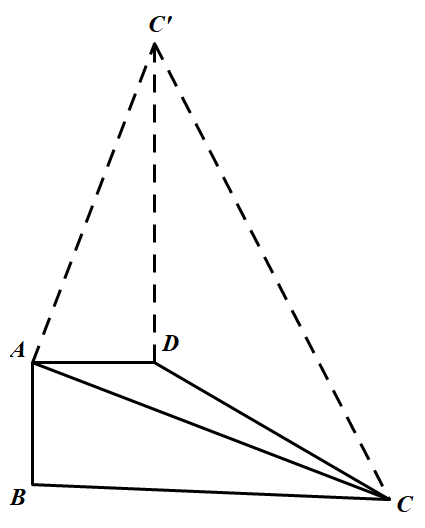
在 $\triangle CDC^{\prime}$ 中,$\angle CDC^{\prime}=120^{\circ}$,设 $DC^{\prime}=BC=a$,$DC=b$,$a+b=12\sqrt{3}$
则 $C^{\prime}C^2=a^2+b^2+ab=(a+b)^2-ab\geqslant \dfrac{3}{4}(a+b)^2=324$,
故 $CC^{\prime}\geqslant 18$
$AC$ 的最小值为 $9\sqrt{2}$.

答案
解析
备注