易知 $x,y,z$ 为实数，且 $0<x<y<z<\dfrac{\pi}{2}$．求证：$$\dfrac{\pi}{2}+2\sin x\cos y+2\sin y\cos z>\sin2x+\sin2y+\sin2z.$$
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
要证明的不等式等价于
$\dfrac{\pi}{4}+\sin x\cos y+\sin y\cos z>\sin x\cos x+\sin y\cos y+\sin z\cos z $
$\Leftrightarrow\dfrac{\pi}{4}>\sin x(\cos x-\cos y)-\sin y(\cos y-\cos z)+\sin z\cos z$．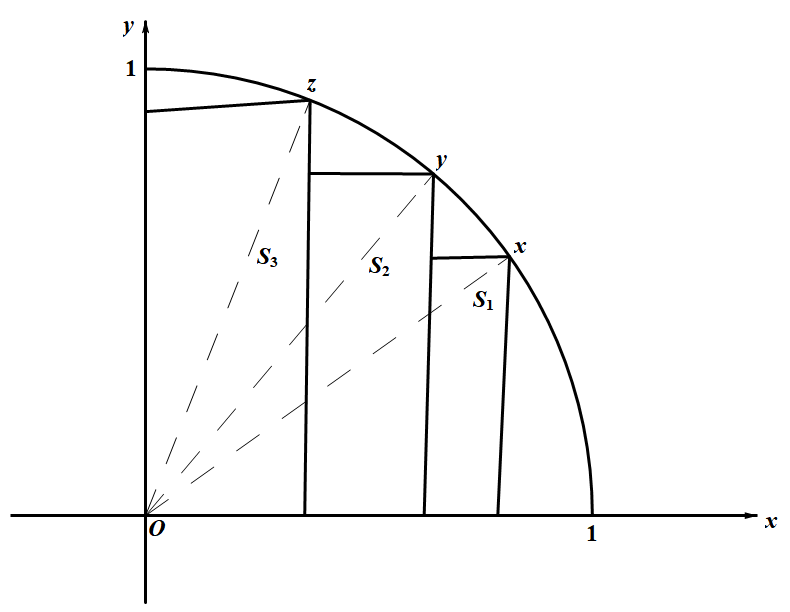
构造图形如图所示，圆 $O$ 是单位圆，$S_1,S_2,S_3$ 分别是三个小矩形的面积，$x,y,z$ 分别表示扇形的圆心角，则 $S_1=\sin x(\cos x-\cos y)$，$S_2=\sin y(\cos y-\cos z)$，$S_3=\sin z\cos z$．
因为 $S_1+S_2+S_3<\dfrac{1}{4}\cdot\pi\cdot 1^2=\dfrac{\pi}{4}$，
所以 $\dfrac{\pi}{4}>\sin x(\cos x-\cos y)-\sin y(\cos y-\cos z)+\sin z\cos z$．
从而原不等式成立．
$\dfrac{\pi}{4}+\sin x\cos y+\sin y\cos z>\sin x\cos x+\sin y\cos y+\sin z\cos z $
$\Leftrightarrow\dfrac{\pi}{4}>\sin x(\cos x-\cos y)-\sin y(\cos y-\cos z)+\sin z\cos z$．
构造图形如图所示，圆 $O$ 是单位圆，$S_1,S_2,S_3$ 分别是三个小矩形的面积，$x,y,z$ 分别表示扇形的圆心角，则 $S_1=\sin x(\cos x-\cos y)$，$S_2=\sin y(\cos y-\cos z)$，$S_3=\sin z\cos z$．因为 $S_1+S_2+S_3<\dfrac{1}{4}\cdot\pi\cdot 1^2=\dfrac{\pi}{4}$，
所以 $\dfrac{\pi}{4}>\sin x(\cos x-\cos y)-\sin y(\cos y-\cos z)+\sin z\cos z$．
从而原不等式成立．
答案
解析
备注
