已知四边形 $ABCD$ 为正方形,在 $D$ 处做线段 $DE=DC$,取 $CE$ 的中点 $F$,连结 $DF$ 与 $AE$ 相交于 $G$,连结 $BG$,已知 $CG=a$,求 $BG+DG$.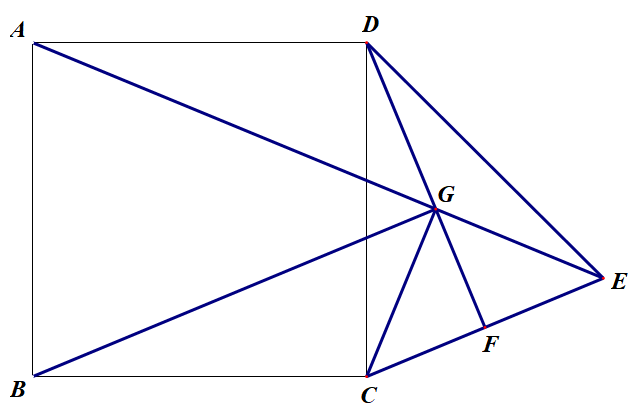

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
简析,由 $DA=DE$,容易得到 $\angle DAG=\angle DEA=\angle DCG$,所以 $D,A,C,G$ 四点共圆,即 $A,B,C,D,G$ 五点共圆,由托勒密定理可知 $DB\cdot CG=BC\cdot DG+DC\cdot BG$,即 $BG+DG=\sqrt{2}a$
答案
解析
备注