在空间四边形 $ABCD$ 中,已知 $AB=a$,$BC=b$,$CD=c$,$DA=d$,求 $\overrightarrow{AC}\cdot\overrightarrow{BD}$.
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
设 $\overrightarrow{AB}=\overrightarrow{a},\overrightarrow{AD}=\overrightarrow{d},\overrightarrow{CD}=\overrightarrow{c},\overrightarrow{CB}=\overrightarrow{b}$,
则 $\overrightarrow{AC}\cdot\overrightarrow{BD}=\overrightarrow{AC}\cdot(\overrightarrow{d}-\overrightarrow{a})\\=\overrightarrow{AC}\cdot\overrightarrow{d}-\overrightarrow{AC}\cdot\overrightarrow{a}=(\overrightarrow{d}-\overrightarrow{c})\cdot\overrightarrow{d}-(\overrightarrow{a}-\overrightarrow{b})\cdot\overrightarrow{a}\\=|\overrightarrow{d}|^2-|\overrightarrow{a}|^2+\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{c}\cdot\overrightarrow{d}$
又 $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{d}-\overrightarrow{c}$,即 $|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{d}|^2+|\overrightarrow{c}|^2-2\overrightarrow{d}\cdot\overrightarrow{c}$
得到 $\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{c}\cdot\overrightarrow{d}=\dfrac{1}{2}(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-|\overrightarrow{c}|^2-|\overrightarrow{d}|^2)$.
所以 $\overrightarrow{AC}\cdot\overrightarrow{BD}=\dfrac{1}{2}(b^2+d^2-a^2-c^2)$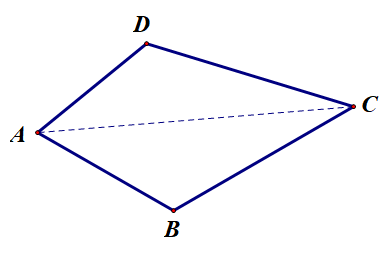
则 $\overrightarrow{AC}\cdot\overrightarrow{BD}=\overrightarrow{AC}\cdot(\overrightarrow{d}-\overrightarrow{a})\\=\overrightarrow{AC}\cdot\overrightarrow{d}-\overrightarrow{AC}\cdot\overrightarrow{a}=(\overrightarrow{d}-\overrightarrow{c})\cdot\overrightarrow{d}-(\overrightarrow{a}-\overrightarrow{b})\cdot\overrightarrow{a}\\=|\overrightarrow{d}|^2-|\overrightarrow{a}|^2+\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{c}\cdot\overrightarrow{d}$
又 $\overrightarrow{a}-\overrightarrow{b}=\overrightarrow{d}-\overrightarrow{c}$,即 $|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-2\overrightarrow{a}\cdot\overrightarrow{b}=|\overrightarrow{d}|^2+|\overrightarrow{c}|^2-2\overrightarrow{d}\cdot\overrightarrow{c}$
得到 $\overrightarrow{a}\cdot\overrightarrow{b}-\overrightarrow{c}\cdot\overrightarrow{d}=\dfrac{1}{2}(|\overrightarrow{a}|^2+|\overrightarrow{b}|^2-|\overrightarrow{c}|^2-|\overrightarrow{d}|^2)$.
所以 $\overrightarrow{AC}\cdot\overrightarrow{BD}=\dfrac{1}{2}(b^2+d^2-a^2-c^2)$

答案
解析
备注