如图,在平面直角坐标系中,方程为 $x^2+y^2+Dx+Ey+F=0$ 的圆 $M$ 的内接四边形 $ABCD$ 的对角线 $AC$ 和 $BD$ 互相垂直,且 $AC$ 和 $BD$ 分别在 $x$ 轴和 $y$ 轴上.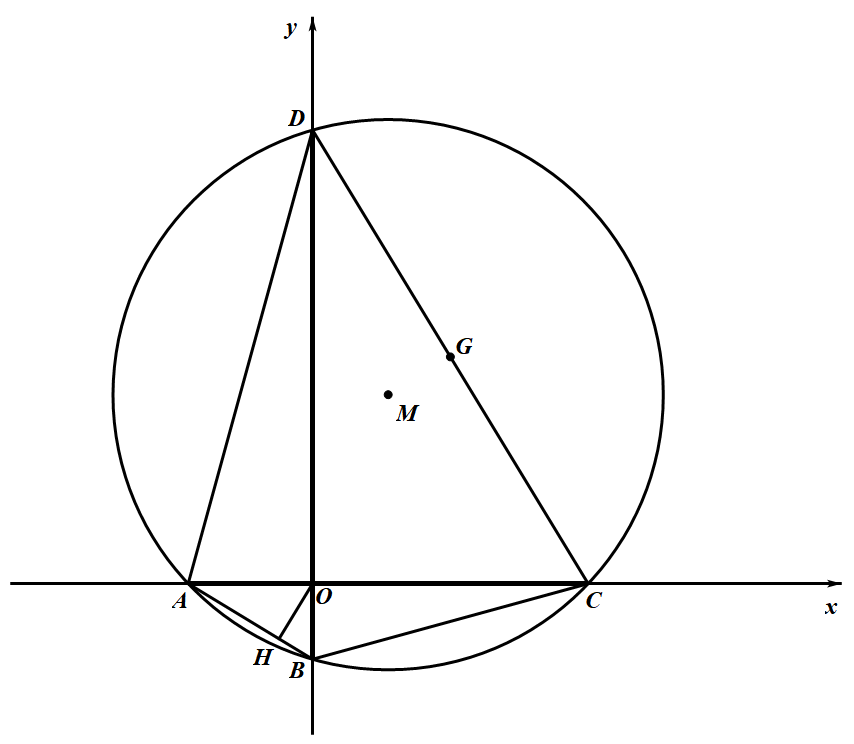

【难度】
【出处】
无
【标注】
-
求证:$F<0$;标注答案略解析略
-
若四边形 $ABCD$ 的面积为 $8$,对角线 $AC$ 的长为 $2$,且 $\overrightarrow{AB}\cdot\overrightarrow{AD}=0$,求 $D^2+R^2-4F$ 的值.标注答案略解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2