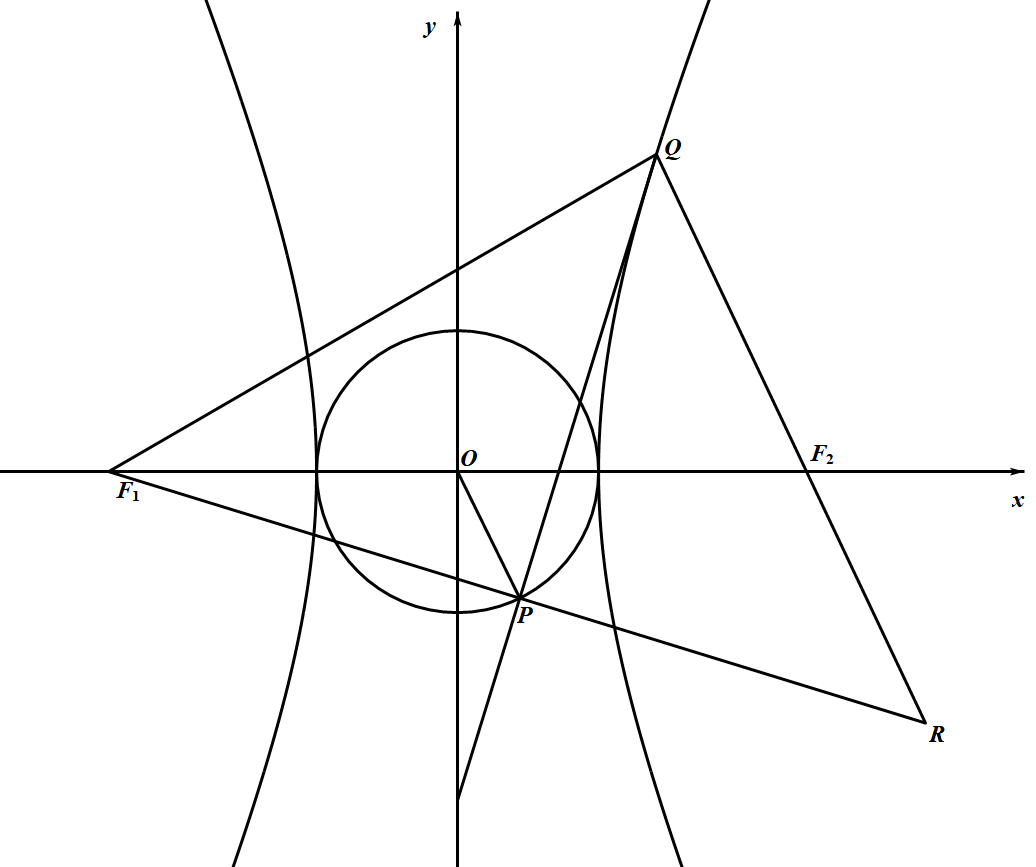
设双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1(a>0,b>0)$ 的两个焦点为 $F_1(-c,0),F_2(c,0)$,点 $Q$ 是双曲线右(或左)支上除顶点外的任一点,从焦点 $F_1$(或 $F_2$)作 $\angle{F_1QF_2}$ 的角分线的垂线,垂足为 $P$,则 $P$ 点的轨迹是以原点为圆心,$a$ 为半径的圆(除去点 $(-a,0),(a,0)$).
【难度】
【出处】
无
【标注】
【答案】
略
【解析】
答案
解析
备注