如图,已知梯形 $ABCD$ 中,$|AB|=2|CD|$,点 $E$ 满足 $\overrightarrow{AE}=\lambda\overrightarrow{EC}$,双曲线 $\dfrac{x^2}{a^2}-\dfrac{y^2}{b^2}=1$ 过 $C,D,E$ 三点,且以 $A,B$ 为焦点,当 $\dfrac{2}{3}\leqslant\lambda\leqslant\dfrac{3}{4}$ 时,求双曲线离心率 $e$ 的取值范围.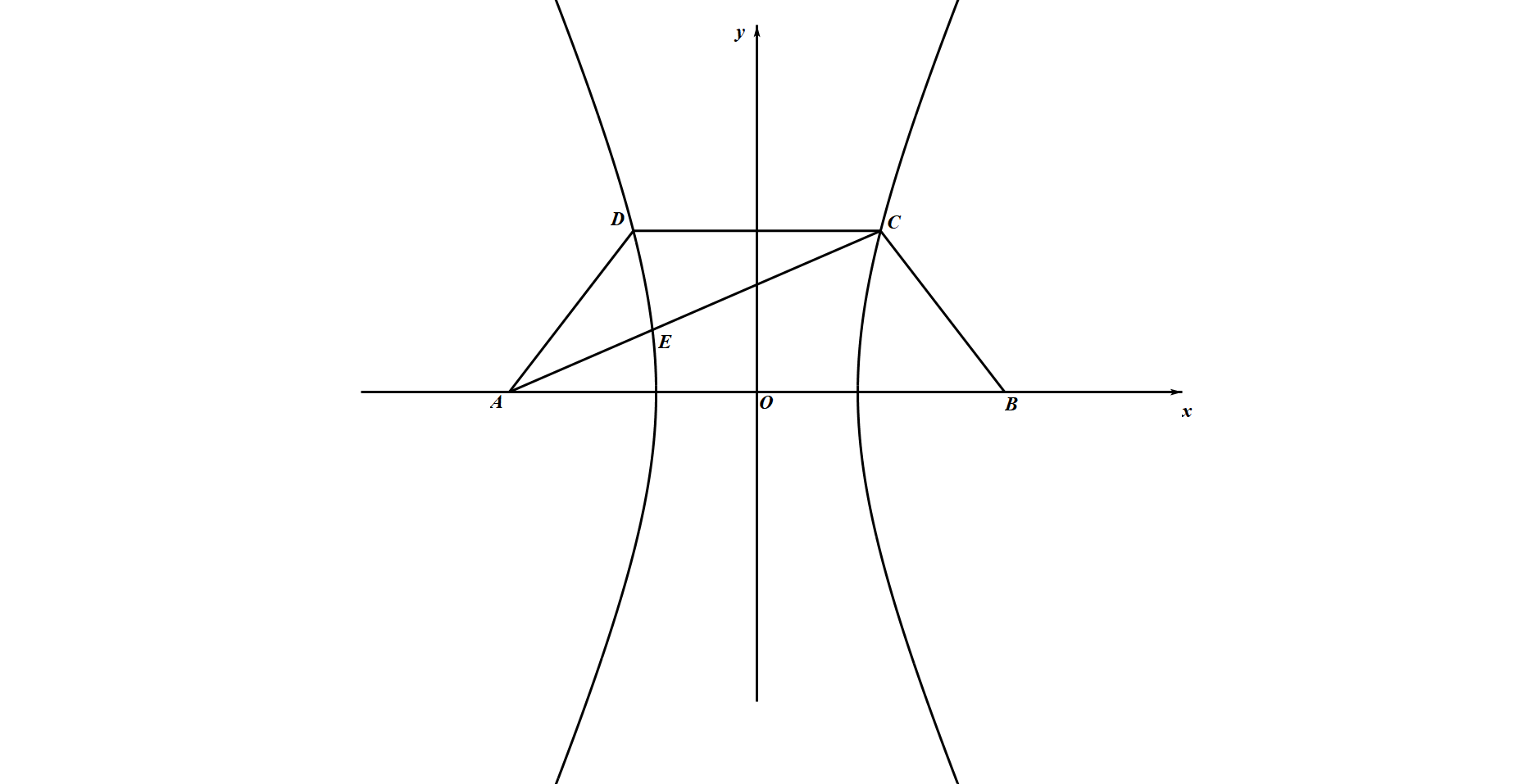

【难度】
【出处】
无
【标注】
【答案】
略
【解析】
略
答案
解析
备注