如图,设点 $P(x_0,y_0)$ 在直线 $x=m(y\ne\pm{m},0<m<1)$ 上,过 $P$ 作双曲线 $x^2-y^2=1$ 的两条切线 $PA$ 和 $PB$,切点为 $A$ 和 $B$,定点 $M\left(\dfrac{1}{m},0\right)$.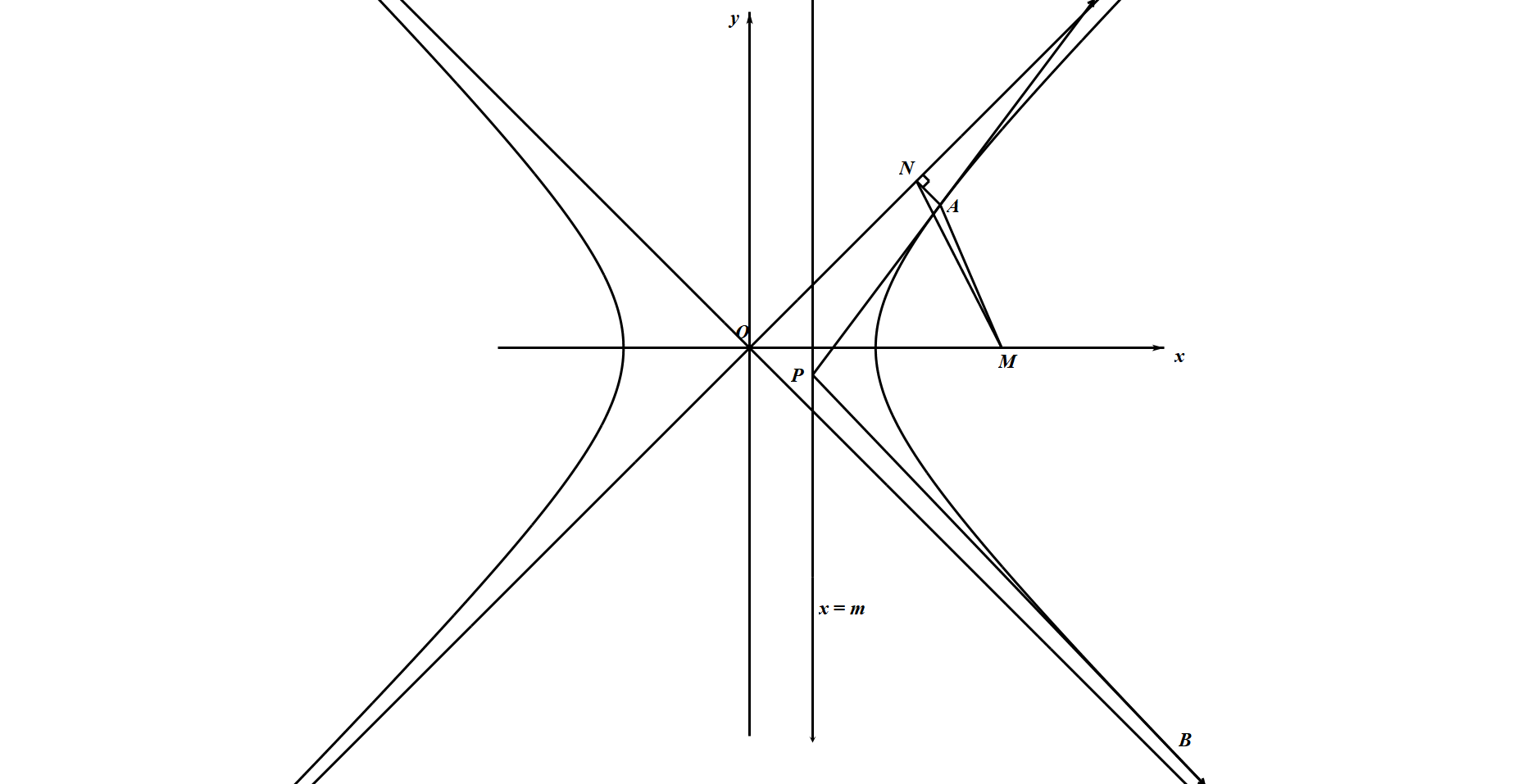

【难度】
【出处】
无
【标注】
-
证明:$A,M,B$ 三点共线;标注答案略解析略
-
过点 $A$ 作直线 $x-y=0$ 的垂线,垂足为 $N$,试求 $\triangle{AMN}$ 的重心 $G$ 所在曲线方程.标注答案略解析略
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2