如图,椭圆 $\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左焦点为 $F$,过点 $F$ 的直线交椭圆于 $A$、$B$ 两点.当直线 $AB$ 经过椭圆的一个顶点时,其倾斜角恰为 $60^{\circ}$.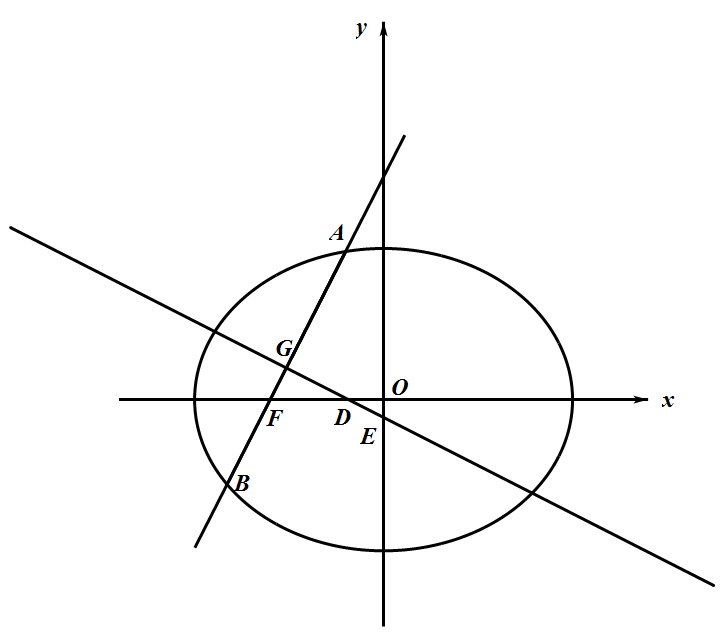

【难度】
【出处】
2018年全国高中数学联赛河北省预赛(高三)
【标注】
-
求该椭圆的离心率标注答案$e=\dfrac{1}{2}$解析依题意,当直线 $AB$ 经过椭圆的顶点 $(0,b)$ 时,其倾斜角为 $60^{\circ}$.设 $F(-c,0)$,则 $\dfrac{b}{c}=\tan 60^{\circ}=\sqrt{3}$.将 $b=\sqrt{3}c$ 代入 $a^{2}=b^{2}+c^{2}$,得 $a=2c$.所以椭圆的离心率 $e=\dfrac{c}{a}=\dfrac{1}{2}$.
-
设线段 $AB$ 的中点为 $G$,$AB$ 的中垂线与 $x$ 轴、$y$ 轴分别交于 $D$、$E$ 两点.记 $\triangle GDF$ 的面积为 $S_{1}$,$\triangle OED$($O$ 坐标原点)的面积为 $S_{2}$,求 $\dfrac{S_{1}}{S_{2}}$ 的取值范围标注答案$(9,+\infty)$解析由(1)知,椭圆方程可设为 $\dfrac{x^2}{4c^2}+\dfrac{y^2}{3c^2}=1$,设 $A(x_{1},y_{1})$,$B(x_{2},y_{2})$.依题意,直线 $AB$ 不能与 $x$、$y$ 轴垂直,故设直线 $AB$ 的方程为 $y=k(x+c)$,将其代入 $3x^{2}+4y^2=12c^2$,整理得 $(4k^2+3)x^2+8ck^{2}x+4k^{2}c^{2}-12c^2=0$.则 $x_{1}+x_{2}=\dfrac{-8ck^2}{4k^{2}+3},y_{1}+y_{2}=\dfrac{6ck}{4k^{2}+3}$.所以 $G(\dfrac{-4ck^2}{4k^{2}+3},\dfrac{3ck}{4k^{2}+3})$.因为 $GD\bot AB$,所以 $\dfrac{\dfrac{3ck}{4k^{2}+3}}{\dfrac{-4ck^2}{4k^{2}+3}-x_{D}}\times k=-1,x_{D}=\dfrac{-ck^2}{4k^{2}+3}$.因为 $\triangle GDF\sim \triangle OED$,所以 $\dfrac{S_{1}}{S_{2}}=\dfrac{|GD|^2}{|OD|^2}=\dfrac{(\dfrac{-4ck^2}{4k^{2}+3}-\dfrac{-ck^2}{4k^{2}+3})^2+(\dfrac{3ck^2}{4k^{2}+3})^2}{(\dfrac{-ck^2}{4k^{2}+3})^2}=\dfrac{(3ck^2)^2+(3ck)^2}{(ck^2)^2}=\dfrac{9c^{2}k^{4}+9c^{2}k^{2}}{c^{2}k^{4}}=9+\dfrac{9}{k^2}>9$.所以 $\dfrac{S_{1}}{S_{2}}$ 的取值范围是 $(9,+\infty)$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2