如图,设 $\triangle ABC$ 的外接圆为 $\odot O$,$\angle BAC$ 的角平分线与 $BC$ 交于点 $D$,$M$ 为 $BC$ 的中点.若 $\triangle ADM$ 的外接圆 $\odot Z$ 分别与 $AB$、$AC$ 交于 $P$、$Q$,$N$ 为 $PQ$ 的中点,证明:$MN\parallel AD$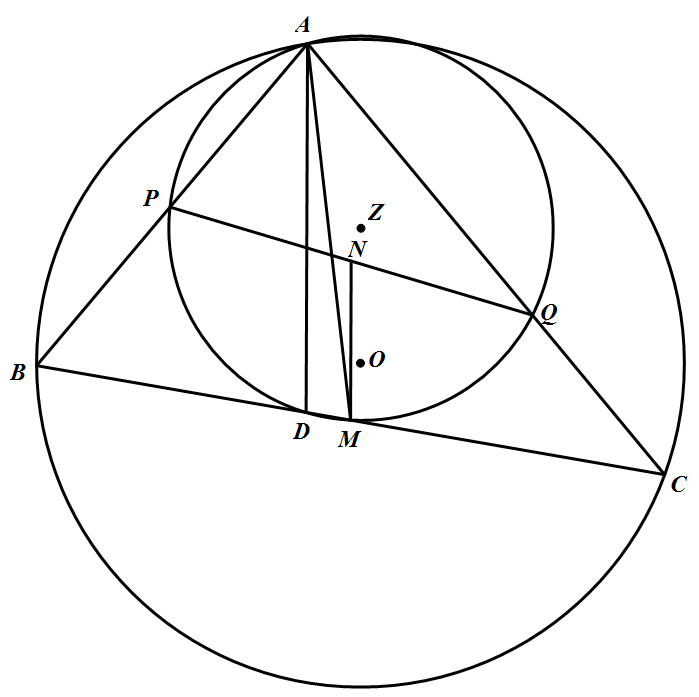

【难度】
【出处】
2018年全国高中数学联赛河北省预赛(高三)
【标注】
【答案】
略
【解析】
设 $AB=c$,$BC=a$,$AC=b$.在 $\triangle ABC$ 中,$AD$ 为 $\angle BAC$ 的平分线,所以 $\dfrac{BD}{DC}=\dfrac{AB}{AC}$,故有 $\dfrac{BD}{BD+DC}=\dfrac{AB}{AB+AC}$,因此有 $\dfrac{BD}{a}=\dfrac{c}{b+c}$,所以 $BD=\dfrac{ac}{b+c}$.又 $BM=\dfrac{a}{2}$,由 $BP\cdot BA=BD\cdot BM$ 得 $BP=\dfrac{BD\cdot BM}{AB}=\dfrac{a^{2}}{2(b+c)}$.由 $CQ\cdot CA=CM\cdot CD$ 得,$CQ=\dfrac{a^{2}}{2(b+c)}$,因此 $CQ=BP$.
如图,连结 $BQ$、$PC$,并设 $X$、$Y$ 分别为 $BQ$、$PC$ 的中点,易证 $XN$ 平行且等于 $MY$,所以四边形 $NXMY$ 为平行四边形.由 $CQ=BP$ 知 $NX=NY$,所以四边形 $NXMY$ 为菱形,从而 $MN$ 平分 $\angle XNY$.又 $AD$ 平分 $\angle BAC$,$AB\parallel NX$,$AC\parallel NY$,所以 $MN\parallel AD$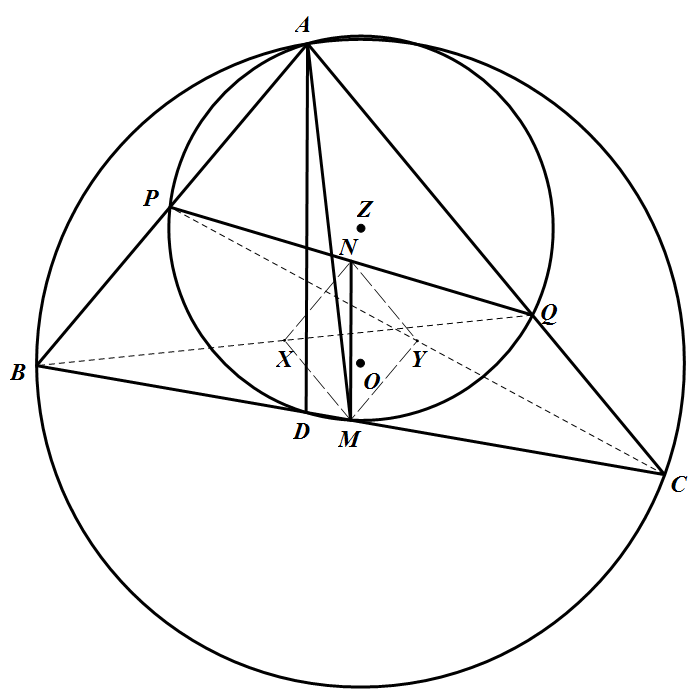
如图,连结 $BQ$、$PC$,并设 $X$、$Y$ 分别为 $BQ$、$PC$ 的中点,易证 $XN$ 平行且等于 $MY$,所以四边形 $NXMY$ 为平行四边形.由 $CQ=BP$ 知 $NX=NY$,所以四边形 $NXMY$ 为菱形,从而 $MN$ 平分 $\angle XNY$.又 $AD$ 平分 $\angle BAC$,$AB\parallel NX$,$AC\parallel NY$,所以 $MN\parallel AD$

答案
解析
备注