如图,园内接四边形 $ABCD$ 中,自 $AD$ 的中点 $M$,作 $MN\bot BC,ME\bot AB,MF\bot CD,N,E,F$ 为垂足
证明:$MN$ 过线段 $EF$ 的中点.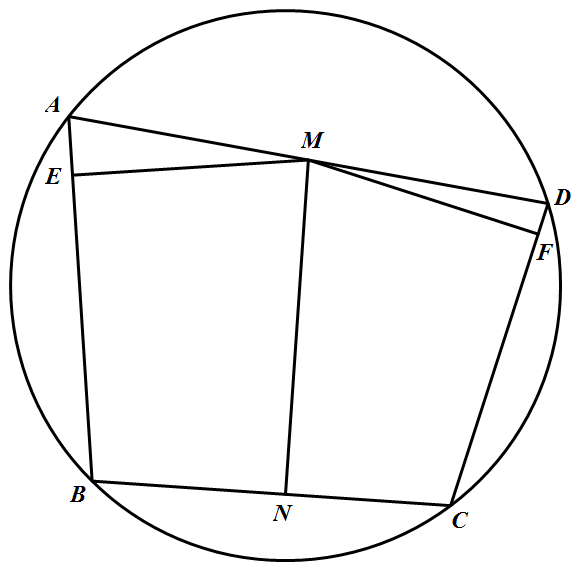
证明:$MN$ 过线段 $EF$ 的中点.

【难度】
【出处】
2018年全国高中数学联赛山西省预赛
【标注】
【答案】
略
【解析】
如图所示,在线段 $AB,CD$ 上分别取点 $G,H$,使 $GE=AE,HF=DF$,则 $A,G,H,D$ 四点共圆(以 $M$ 点为该圆的圆心)所以 $\angle BGH=\angle ADC=180^{\circ}-\angle ABC$,于是 $GH\parallel BC$,则 $MN\bot GH$.设垂足为 $K$,于是 $K$ 为 $GH$ 的中点(圆心 $M$ 至圆弦的垂线,平分该弦),这样就有 $E,K,F,M$ 为四边形 $AGHD$ 四条边的中点,因此四边形 $EKFM$ 为平行四边形,故其对角线互相平分,即 $MN$ 过线段 $EF$ 的中点.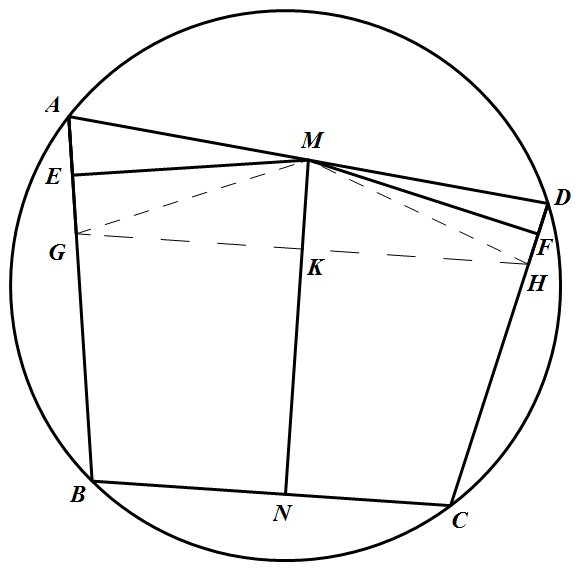

答案
解析
备注