查看数据源：5cb85012210b280220ed2141
如图，圆 $O_{1}$，圆 $O_{2}$ 与圆 $O_{3}$ 相交于点 $P$，圆 $O_{1}$ 和圆 $ O_{2} $ 的另一个点为 $ A $．经过点 $ A $ 的一条直线分别交于圆 $ O_{1} $，圆 $ O_{2} $ 于点 $ B,C $，$ AP $ 的延长线交圆 $ O_{3} $ 于点 $ D $．作 $ DE\parallel BC $ 交圆 $ O_{3} $ 于点 $ E $，再作 $ EM,EN $ 分别切于圆 $ O_{1} $、圆 $ O_{1} $ 于点 $ M,N $，求证：$ EM^2-EN^2=DE\cdot BC$．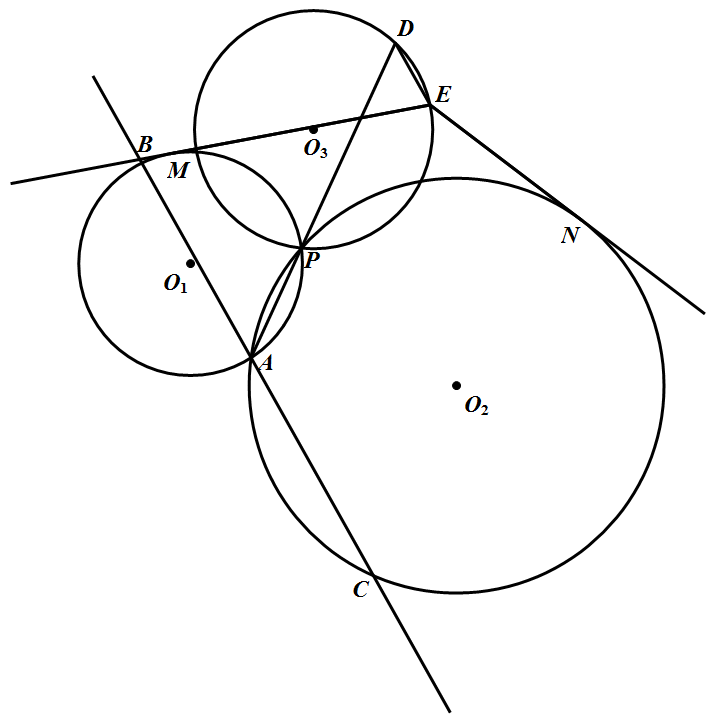
【难度】
【出处】
2018年全国高中数学联赛辽宁省预赛
【标注】
  • 知识点
    >
    解析几何
    >
    直线与圆
    >
    圆的切线方程
  • 知识点
    >
    解析几何
    >
    直线与圆
    >
    圆与圆的位置关系
【答案】
略
【解析】
连结 $EP$，分别与圆 $O_{1}$、圆 $O_{2}$、$BC$ 相交于点 $S,T,Q$，则由相交弦定理及切割线定理得：$QA\cdot QB=QS\cdot QP,QA\cdot QC=QT\cdot QP$．两式相加得：$QA\cdot BC=ST\cdot QP\Rightarrow\dfrac{BC}{ST}=\dfrac{QP}{QA}$．又 $DE\parallel BC$，所以 $\triangle AQP\sim\triangle DEP,\dfrac{QP}{QA}=\dfrac{EP}{ED}$．因此 $\dfrac{BC}{ST}=\dfrac{QP}{QA}=\dfrac{EP}{ED}$，故 $DE\cdot BC=EP\cdot ST=EP\cdot (ES-ET)=EP\cdot ES-EP\cdot ET=EM^2-EN^2$．
答案 解析 备注
0.110019s