如图,在锐角 $\triangle ABC$ 中,$D,E$ 是边 $BC$ 上的点,$\triangle ABC,\triangle ABD,\triangle ADC$ 的外心分别为 $O,P,Q$.证明: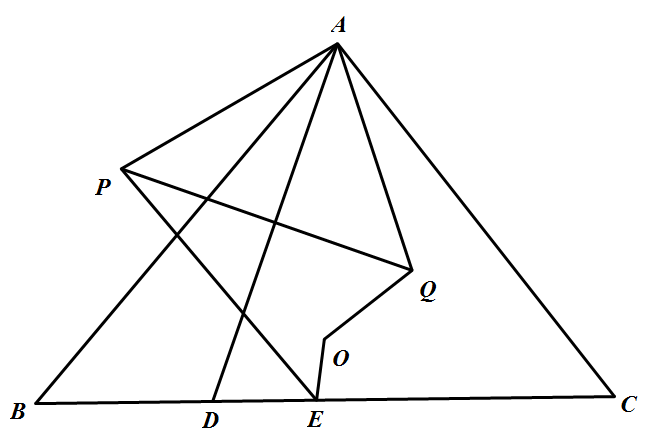

【难度】
【出处】
2018年全国高中数学联赛福建省预赛
【标注】
-
$\triangle APQ\sim\triangle ABC$.标注答案略解析如图,连结 $PD,QD$.因为 $P,Q$ 分别为 $\triangle ABD,\triangle ADC$ 的外心,所以 $PQ$ 为线段 $AD$ 的垂直平分线.所以 $\angle APQ=\dfrac{1}{2}\angle APD=\angle ABD=\angle ABC,\angle AQP=\dfrac{1}{2}\angle AQD=\angle ACD=\angle ACB$.故 $\triangle APQ\sim\triangle ABC$.

-
若 $EO\bot PQ$,则 $QO\bot PE$.标注答案略解析如图,连结 $OA,OB,OP,PB,QC$.延长 $OQ$ 与 $AC$ 相交于点 $F$.由 $O,P,Q$ 分别为 $\triangle ABC,\triangle ABD,\triangle ADC$ 的外心,知 $OP,OQ,PQ$ 分别是线段 $AB,AC,AD$ 的垂直平分线.所以 $\angle APB=\angle APD+\angle BPD=2(\angle ABD+\angle BAD)=2\angle ADC=\angle AQC$.又 $\angle OBP=\angle OAP,\angle AQF=\dfrac{1}{2}\angle AQC=\dfrac{1}{2}\angle APB=\angle APBO$.所以 $A,P,O,Q$ 四点共圆,$\angle OAP=\angle OQP$.又 $EO\bot PQ,DA\bot PQ$,所以 $EO\parallel DA$,$\angle OEC=\angle ADC=\dfrac{1}{2}\angle APB=\angle BPO$.所以 $P,B,E,Q$ 四点共圆,$\angle OEP=\angle OBP$.设 $EO,QO$ 的延长线分别与 $PQ,PE$ 相交于 $M,N$,则 $\angle OEP=\angle OBP=\angle OAP=\angle OQP$.故 $M,N,E,Q$ 四点共圆.又 $EO\bot PQ$,所以 $\angle QNE=\angle QME=90^\circ$.故 $QO\bot PE$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2