如图，$\triangle ABC$ 的内心为 $I,D,E,F$ 分别是边 $BC,CA,AB$ 的中点，证明：直线 $DI$ 平分 $\triangle DEF$ 的周长．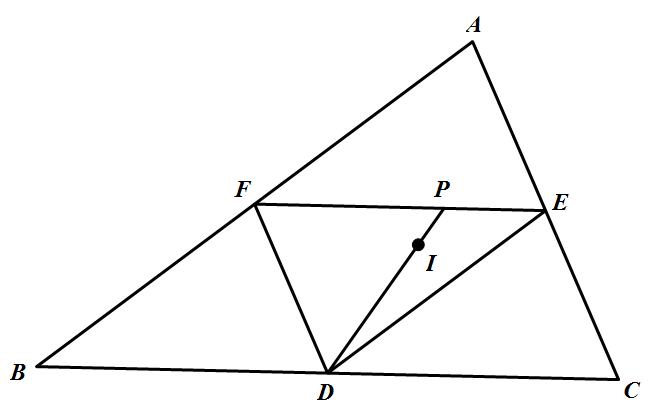
【难度】
【出处】
2018年全国高中数学联赛江西省预赛
【标注】
【答案】
略
【解析】
如图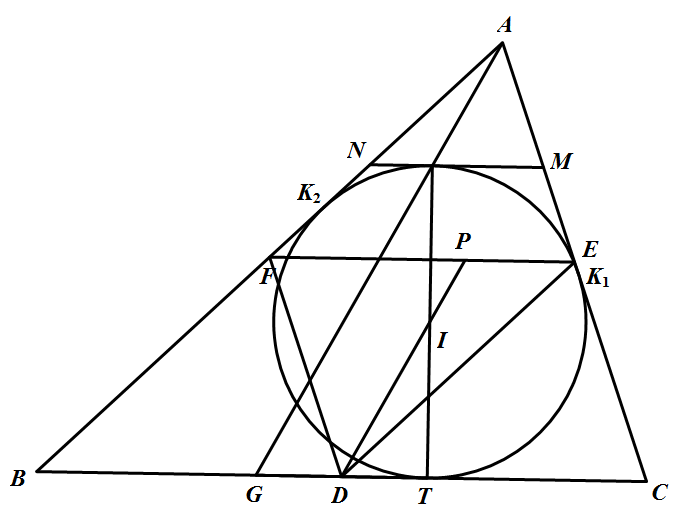
，不妨设 $AB\geqslant AC$，$\triangle ABC$ 的内切圆切 $BC,CA,AB$ 于 $T,K_1,K_2$．过 $T$ 作内切圆的直径 $TK$，过 $K$ 作 $\odot I$ 的切线分别交 $AC,AB$ 于 $M,N$，则 $NM\parallel BC$．
由于 $\odot I$ 是 $\triangle AMN$ 的旁切圆，$AK_1=AK_2$，因 $MK=MK_1,NK=NK_2$，所以有 $AM+MK=AN+NK$．延长 $AK$ 交 $BC$ 于 $G$，则 $BG=CT$，因此 $DT=DG$，故 $DI$ 是 $\triangle TGK$ 的中位线，所以 $DP\parallel AG$，因四边形 $BDEF$ 为平行四边形，所以 $\triangle DEP\sim\triangle ABG$，相似比为 $\dfrac{DE}{AB}=\dfrac{1}{2}$．同理，$\triangle DEP\sim\triangle ACG$，相似比为 $\dfrac{DF}{AC}=\dfrac{1}{2}$．又注意 $\triangle AMK\sim\triangle ACG,\triangle ANK\sim\triangle ABG$，相似比均为 $\dfrac{AK}{AG}$，既然有 $AM+MK=AN+NK$，所以 $AC+CG=AB+BG$，因此，$DF+FP=DE+EP$，即所证结论成立．
，不妨设 $AB\geqslant AC$，$\triangle ABC$ 的内切圆切 $BC,CA,AB$ 于 $T,K_1,K_2$．过 $T$ 作内切圆的直径 $TK$，过 $K$ 作 $\odot I$ 的切线分别交 $AC,AB$ 于 $M,N$，则 $NM\parallel BC$．由于 $\odot I$ 是 $\triangle AMN$ 的旁切圆，$AK_1=AK_2$，因 $MK=MK_1,NK=NK_2$，所以有 $AM+MK=AN+NK$．延长 $AK$ 交 $BC$ 于 $G$，则 $BG=CT$，因此 $DT=DG$，故 $DI$ 是 $\triangle TGK$ 的中位线，所以 $DP\parallel AG$，因四边形 $BDEF$ 为平行四边形，所以 $\triangle DEP\sim\triangle ABG$，相似比为 $\dfrac{DE}{AB}=\dfrac{1}{2}$．同理，$\triangle DEP\sim\triangle ACG$，相似比为 $\dfrac{DF}{AC}=\dfrac{1}{2}$．又注意 $\triangle AMK\sim\triangle ACG,\triangle ANK\sim\triangle ABG$，相似比均为 $\dfrac{AK}{AG}$，既然有 $AM+MK=AN+NK$，所以 $AC+CG=AB+BG$，因此，$DF+FP=DE+EP$，即所证结论成立．
答案
解析
备注
