查看数据源：599165c12bfec200011e00ae
已知椭圆 $C:\dfrac{x^2}
{a^2} + \dfrac{y^2}
{b^2} = 1\left(a > b > 0\right)$ 的左焦点为 $F$，$C $ 与过原点的直线相交于 $A,B $ 两点，连接 $ AF,BF$，若 $|AB|=10$，$|BF|=8$，$\cos \angle ABF =\dfrac 4 5 $，则椭圆 $ C$ 的离心率为 \((\qquad)\)
A: $\dfrac 3 5 $
B: $\dfrac 5 7 $
C: $\dfrac 4 5 $
D: $\dfrac 6 7 $
【难度】
【出处】
2013年高考辽宁卷（文）
【标注】
  • 知识点
    >
    解析几何
    >
    椭圆
    >
    椭圆的几何量
    >
    椭圆的基本量
【答案】
B
【解析】
如图，设 $F'$ 为椭圆 $C$ 的右焦点，连接 $AF',BF'$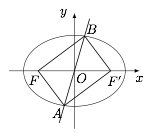．在 $\triangle ABF$ 中，由余弦定理可得\[|AF|=6.\]所以\[\angle AFB=90^\circ.\]设椭圆的右焦点为 $F'$，连接 $BF',AF'$，则由椭圆的对称性可知四边形 $AFBF'$ 为矩形，所以\[|BF'|=|AF|=6,2c=|FF'|=|AB|=10.\]根据椭圆的定义可得\[2a=|BF|+|BF'|=14,\]所以椭圆的离心率\[e=\dfrac ca=\dfrac 57.\]
题目 答案 解析 备注
0.110066s