如图,圆 $C$ 与 $x$ 轴相切于点 $T(2,0)$,与 $y$ 轴的正半轴相交于 $A,B$ 两点($A$ 在 $B$ 的上方),且 $|AB|=3$.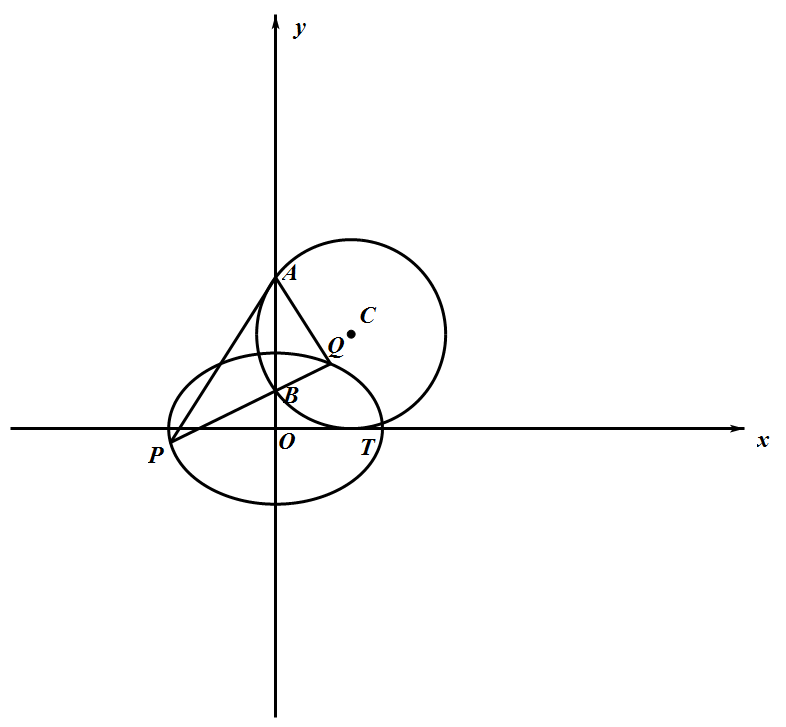

【难度】
【出处】
2018年全国高中数学联赛陕西省预赛(第二试)
【标注】
-
求圆 $C$ 的方程;标注答案$(x-2)^2+(y-\dfrac{5}{2})^2=\dfrac{25}{4}$解析由题设知,圆心 $C$ 到 $AB$ 的距离为 $2$,则圆 $C$ 的半径为 $r=\sqrt{2^2+(\dfrac{|AB|}{2})^2}=\dfrac{5}{2}$.因为圆 $C$ 与 $x$ 轴相切于点 $T(2,0)$,所以圆心 $C$ 的坐标为 $(2,\dfrac{5}{2})$,故圆 $C$ 的方程为 $(x-2)^2+(y-\dfrac{5}{2})^2=\dfrac{25}{4}$.
-
设过点 $B$ 的直线 $l$ 与椭圆 $\dfrac{x^2}{8}+\dfrac{y^2}{4}=1$ 相交于 $P,Q$ 两点,求证:射线 $AB$ 平分 $\angle PAQ$.标注答案略解析在圆 $C$ 的方程中,令 $x=0$,得 $y=4$ 或 $y=1$.所以有 $A(0,4),B(0,1)$.当 $l\bot x$ 轴时,$\angle PAB=\angle QAB=0^\circ$.当 $l$ 与 $x$ 轴不垂直时,设 $l:y=kx+1$,代入 $\dfrac{x^2}{8}+\dfrac{y^2}{4}=1$,得 $(1+2k^2)x^2+4kx-6=0$.设 $P(x_1,y_1),Q(x_2,y_2)$,则 $x_1+x_2=-\dfrac{4k}{1+2k^2},x_1x_2=-\dfrac{6}{1+2k^2}$.所以.所以 ${{k}_{AP}}+{{k}_{AQ}}=\dfrac{{{y}_{1}}-4}{{{x}_{1}}}+\dfrac{{{y}_{2}}-4}{{{x}_{2}}}=\dfrac{k{{x}_{1}}-3}{{{x}_{1}}}+\dfrac{k{{x}_{2}}-3}{{{x}_{2}}}=2k-3\left(\dfrac{1}{{{x}_{1}}}+\dfrac{1}{{{x}_{2}}} \right)=2k-\dfrac{3\left({{x}_{1}}+{{x}_{2}} \right)}{{{x}_{1}}{{x}_{2}}}=2k-\dfrac{-12k}{-6}=0$ 直线 $AP,AQ$ 的倾斜角互补,则 $\angle PAB=\angle QAB$.综上,射线 $AB$ 平分 $\angle PAQ$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2