如图，在锐角 $\triangle ABC$ 中．$M$ 是 $BC$ 的中点，圆 $O$ 过点 $A$ 且与直线 $BC$ 相切于点 $C$，直线 $AM$ 与圆 $O$ 交于另一点 $D$，直线 $BD$ 与圆 $O$ 交于另一点 $E$．
证明：$\angle EAC=\angle BAC$．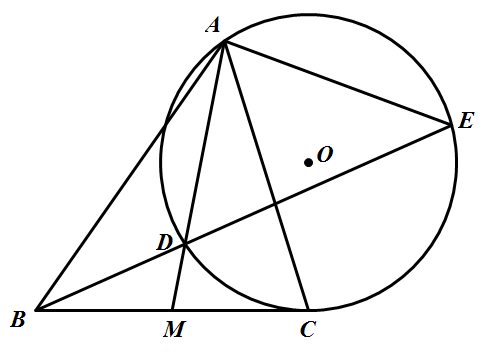
证明：$\angle EAC=\angle BAC$．
【难度】
【出处】
2018年全国高中数学联赛陕西省预赛（第二试）
【标注】
【答案】
略
【解析】
如图，连结 $CE$，则 $\angle ACE=\angle ADE=\angle BDM$．因为圆 $O$ 与直线 $BC$ 相切于点 $C$，$M$ 为 $BC$ 的中点，所以 $BM^2=MC^2=MD\cdot MA$，即 $\dfrac{BM}{MD}=\dfrac{MA}{BM}$．又 $\angle BMD=\angle AMB$，所以 $\triangle BMD\sim \triangle AMB$．所以 $\angle BDM=\angle ABM$．从而 $\angle ACE=\angle ABC$．又 $BC$ 与圆 $O$ 相切，所以 $\angle AEC=\angle ACB$．所以 $\triangle ACE\sim \triangle ABC$，故 $\angle EAC=\angle BAC$．
答案
解析
备注
