如图 ① 所示，已知四边形 $ABCD$ 满足 $AD\parallel BC$，$BA=AD=DC=\dfrac{1}{2}BC=a$，$E$ 是 $BC$ 的中点．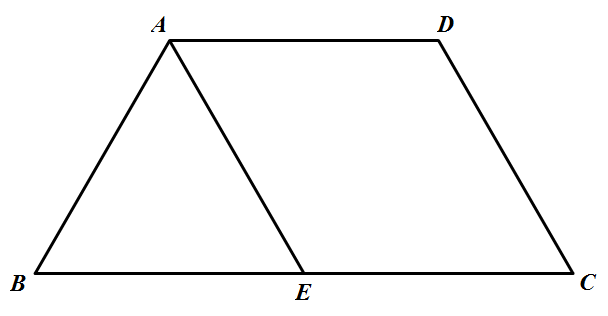
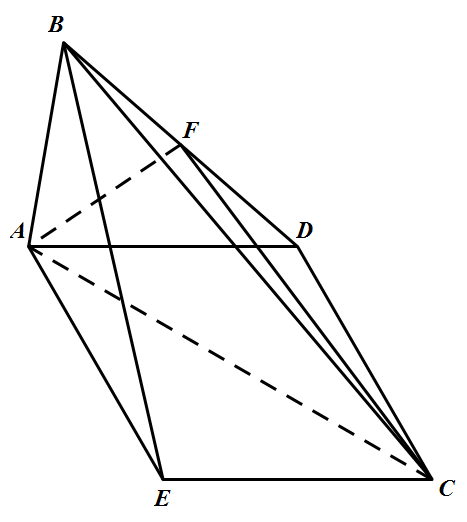
将 $\triangle BAE$ 沿着 $AE$ 翻折成 $B_1AE$，使面 $B_1AE\bot $ 面 $AECD$，$F$ 为 $B_1D$ 的中点，如图 ② 所示．
将 $\triangle BAE$ 沿着 $AE$ 翻折成 $B_1AE$，使面 $B_1AE\bot $ 面 $AECD$，$F$ 为 $B_1D$ 的中点，如图 ② 所示．【难度】
【出处】
2018年全国高中数学联赛甘肃省预赛
【标注】
-
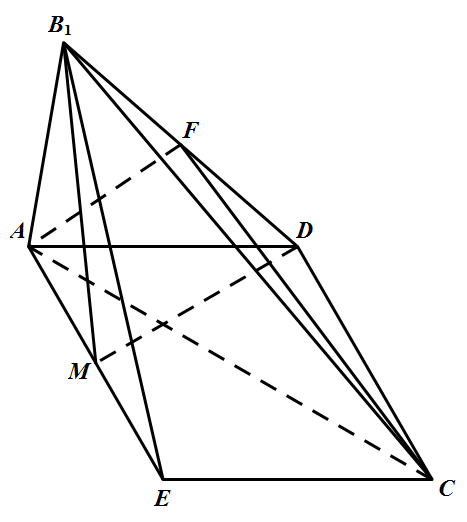
求四棱锥 $B_1-AECD$ 的体积；标注答案$V=\dfrac{a^3}{4}$解析如图所示，取 $AE$ 的中点 $M$，连结 $B_1M$．因为 $BA=AD=DC=\dfrac{1}{2}BC=a$，$\triangle ABE$ 为等边三角形，则 $B_1M=\dfrac{\sqrt{3}}{2}a$．又因为面 $B_1AE\bot$ 面 $AECD$，所以 $V=\dfrac{1}{3}\times\dfrac{\sqrt{3}}{2}a\times a\times a\times\sin\dfrac{\pi}{3}=\dfrac{a^3}{4}$．
-
求平面 $ADB_1$ 与平面 $ECB_1$ 所成角的正弦值．标注答案$\dfrac{4}{5}$解析连结 $MD$，分别以 $ME,MD,MB_1$ 为 $x,y,z$ 轴，建立空间直角坐标系，则 $E\left(\dfrac{a}{2},0,0 \right),C\left( a,\dfrac{\sqrt{3}}{2}a,0 \right),A\left( -\dfrac{a}{2},0,0\right),D\left( 0,\dfrac{\sqrt{3}}{2}a,0 \right),{{B}_{1}}\left( 0,0,\dfrac{\sqrt{3}}{2}a\right),\\\overrightarrow{EC}=\left( \dfrac{a}{2},\dfrac{\sqrt{3}a}{2},0 \right),\overrightarrow{E{{B}_{1}}}=\left(-\dfrac{a}{2},0,\dfrac{\sqrt{3}a}{2} \right),\overrightarrow{AD}=\left( \dfrac{a}{2},\dfrac{\sqrt{3}a}{2},0\right),\overrightarrow{A{{B}_{1}}}=\left( \dfrac{a}{2},0,\dfrac{\sqrt{3}a}{2}\right).$
设面 $ECB_1$ 的法向量 $\overrightarrow{v}=(x^\prime,y^\prime,z^\prime)$，那么有 $\begin{cases}
\dfrac{a}{2}x^\prime+\dfrac{\sqrt{3}}{2}ay^\prime=0\\
-\dfrac{a}{2}x^\prime+\dfrac{\sqrt{3}}{2}az^\prime=0\\
\end{cases}$ 令 $x^\prime=1$，则 $\overrightarrow{u}=(1,-\dfrac{\sqrt{3}}{3},\dfrac{\sqrt{3}}{3})$．
设面 $ADB_1$ 的法向量 $\overrightarrow{u}=(x,y,z)$，那么有 $\begin{cases}
\dfrac{a}{2}x+\dfrac{\sqrt{3}}{2}ay=0\\
-\dfrac{a}{2}x+\dfrac{\sqrt{3}}{2}az=0\\
\end{cases}$ 令 $x=1$，则 $\overrightarrow{v}=(1,-\dfrac{\sqrt{3}}{3},-\dfrac{\sqrt{3}}{3})$．
得到 $\cos\left\langle \overrightarrow{u},\overrightarrow{v} \right\rangle =\dfrac{1+\dfrac{1}{3}-\dfrac{1}{3}}{\sqrt{1+\dfrac{1}{3}+\dfrac{1}{3}}\times\sqrt{1+\dfrac{1}{3}+\dfrac{1}{3}}}=\dfrac{3}{5}$，所以二面角的正弦值为 $\dfrac{4}{5}$．
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
