如图,在 $\triangle ABC$ 中,$\angle C=90^\circ,\angle ABC$ 的平分线交 $AC$ 于点 $E$,过点 $E$ 作 $BE$ 的垂线交 $AB$ 于点 $F$,$\odot O$ 是 $\triangle BEF$ 的外接圆且 $\odot O$ 交 $BC$ 于点 $D$.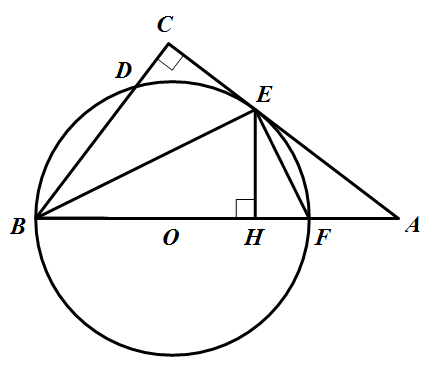

【难度】
【出处】
2018年全国高中数学联赛黑龙江省预赛
【标注】
-
求证:$AC$ 是 $\odot O$ 的切线;标注答案略解析如图 ①,连结 $OE$.因为 $BE$ 平分 $\angle ABC$,所以 $\angle CBE=\angle OBE$,又 $OB=OE$,所以 $\angle OBE=\angle OEB$,所以 $\angle OEB=\angle CBE$,故 $OE\parallel BC$,所以 $\angle AEO=\angle C=90^\circ$,所以 $AC$ 是 $\odot O$ 的切线.

-
过点 $E$ 作 $EH\bot AB$,垂足为 $H$,求证:$CD=HF$标注答案略解析如图 ②,连结 $DE$.因为 $\angle CBE=\angle OBE,EC\bot BC$ 与 $C$,$EH\bot AB$ 于 $H$,所以 $EC=EH$.又 $\angle CDE+\angle BDE=180^\circ,\angle HFE+\angle BDE=180^\circ$,所以 $\angle CDE=\angle HFE$.在 $\triangle CDE$ 与 $\triangle HFE$ 中,$\begin{cases}
\angle CDE=\angle HFE\\
\angle C=\angle EHF=90^\circ\\
EC=EH\\
\end{cases}$ 所以 $\triangle CDE\cong\triangle HFE(AAS)$,故 $CD=HF$.
-
在(2)的条件下,若 $CD=1,EH=3$,求 $BF$ 及 $AF$ 的长.标注答案$BF=10,AF=\dfrac{5}{4}$解析由(2)得,$CD=HF$.又 $CD=1$,所以 $HF=1$,在 $Rt\triangle HFE$ 中,$EF=\sqrt{3^2+1^2}=\sqrt{10}$.因为 $EF\bot BE$,所以 $\angle BEF=90^\circ$,所以 $\angle EHF=\angle BEF=90 ^\circ$.又 $\angle EFH=\angle BFE$,故 $\triangle EHF\sim \triangle BEF$.所以 $\dfrac{EF}{BF}=\dfrac{HF}{EF}$,即 $\dfrac{\sqrt{10}}{BF}=\dfrac{1}{\sqrt{10}}$,所以 $BF=10$.又 $OE=\dfrac{1}{2}BF=5,OH=5-1=4$,所以在 $Rt\triangle OHE$ 中,$\cos\angle EOA=\dfrac{4}{5}$,所以在 $Rt\triangle EOA$ 中,$\cos\angle EOA=\dfrac{OE}{OA}=\dfrac{4}{5}$,故 $\dfrac{5}{OA}=\dfrac{4}{5}$,有 $OA=\dfrac{25}{4}$,所以 $AF=\dfrac{25}{4}-5=\dfrac{5}{4}$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3