已知梯形 $ABCD$,边 $CD,AB$ 分别为上,下底,且 $\angle ADC=90^\circ$,对角线 $AC\bot BD$,过 $D$ 作 $DE\bot BC$ 于点 $E$.证明: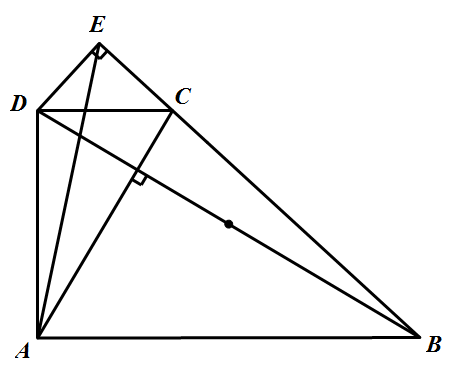

【难度】
【出处】
2018年全国高中数学联赛贵州省预赛
【标注】
-
$AC^2=CD^2+AB\cdot CD$标注答案略解析由于 $\angle ADC=90^\circ$,故 $AC^2=CD^2+AD^2$.因为对角线 $AC\bot BD$,所以 $\angle DCA=90^\circ-\angle BDC=\angle ADB$.而 $\angle ADC=90^\circ=\angle BAD$,则 $\triangle ACD\sim \triangle BDA$,故 $\dfrac{AD}{CD}=\dfrac{AB}{AD}\Rightarrow AD^2=AB\cdot CD$.
-
$\dfrac{AE}{BE}=\dfrac{AC\cdot CD}{AC^2-CD^2}$标注答案略解析由于 $\angle ADC=90^\circ$,故 $AC^2-CD^2=AD^2$,所以 $\dfrac{AC\cdot CD}{A{{C}^{2}}-C{{D}^{2}}}=\dfrac{AC\cdot CD}{A{{D}^{2}}}=\dfrac{AC\cdot CD}{AB\cdot CD}=\dfrac{AC}{AB}$.因为 $\angle BAD+\angle DEB=180^\circ$,所以 $A,B,E,D$ 四点公园,如图所示,故 $\angle AEB=\angle ADB$.由于 $\angle BAC=90^\circ-\angle, CAD=\angle ADB$,且 $\angle AEB=\angle BAC,\angle EBA=\angle ABC$,则 $\triangle ABE\sim\triangle CBA$,故 $\dfrac{AE}{BE}=\dfrac{CA}{AB}$.所以 $\dfrac{AE}{BE}=\dfrac{AC\cdot CD}{AC^2-CD^2}$.

题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2