证明
【难度】
【出处】
2018年全国高中数学联赛贵州省预赛
【标注】
-
$\dfrac{1}{2^k}+\dfrac{1}{2^k+1}+\dfrac{1}{2^k+2}+\cdots+\dfrac{1}{2^{k+1}-1}<1(k\geqslant 2,k\in\mathbf N)$标注答案略解析$\dfrac{1}{2^k}+\dfrac{1}{2^k+1}+\dfrac{1}{2^k+2}+\cdots+\dfrac{1}{2^{k+1}-1}<\underbrace{\frac{1}{{{2}^{k}}}+\frac{1}{{{2}^{k}}}+\cdots+\frac{1}{{{2}^{k}}}}_{{{2}^{k}个}}=\dfrac{2^k}{2^k}=1$.
-
分别以 $1,\dfrac{1}{2},\dfrac{1}{3},\cdots,\dfrac{1}{n},\cdots$ 为边长的正方形,能互不重叠地全部放入一个边长为 $\dfrac{3}{2}$ 的正方形内.标注答案略解析由(1)知,$\dfrac{1}{2^k}+\dfrac{1}{2^k+1}+\dfrac{1}{2^k+2}+\cdots+\dfrac{1}{2^{k+1}-1}<1$,故以边长为 $\dfrac{1}{2^k},\dfrac{1}{2^k+1},\dfrac{1}{2^k+2},\cdots,\dfrac{1}{2^{k+1}-1}$ 的正方形可以并排放入底为 $1$,高为 $\dfrac{1}{2^k}$ 的矩形内,而不重叠.取 $k=2,3,4,\cdots$,即得底分别为 $\dfrac{1}{2^2}+\dfrac{1}{2^2+1}+\cdots+\dfrac{1}{2^3-1},\dfrac{1}{2^3}+\dfrac{1}{2^3+1}+\cdots+\dfrac{1}{2^4-1},\dfrac{1}{2^4}+\dfrac{1}{2^4+1}+\cdots+\dfrac{1}{2^5-1},\cdots$,
高分别为 $\dfrac{1}{2^2},\dfrac{1}{2^3},\dfrac{1}{2^4},\cdots$ 的一系列矩形,这些矩形的底小于 $1$,高的和为 $\dfrac{1}{{{2}^{2}}}+\dfrac{1}{{{2}^{3}}}+\dfrac{1}{{{2}^{4}}}+\cdots=\lim\limits_{n \to \infty}\dfrac{\dfrac{1}{{{2}^{2}}}\left( 1-\dfrac{1}{{{2}^{n}}}\right)}{1-\dfrac{1}{2}}=\lim\limits_{n \to \infty} \dfrac{1}{2}\left(1-\dfrac{1}{{{2}^{n}}} \right)<\dfrac{1}{2}$.因此,以 $1,\dfrac{1}{2},\dfrac{1}{3},\cdots,\dfrac{1}{n},\cdots$ 为边长的正方形中,除了边长为 $1,\dfrac{1}{2},\dfrac{1}{3}$ 的正方形外,其余的正方形全部可以放入底为 $1$,高为 $\dfrac{1}{2}$ 的矩形中(图中阴影部分).而边长 $1,\dfrac{1}{2},\dfrac{1}{3}$ 的三个正方形显然可以放入底为 $\dfrac{3}{2}$,高为 $1$ 的矩形为(如图所示).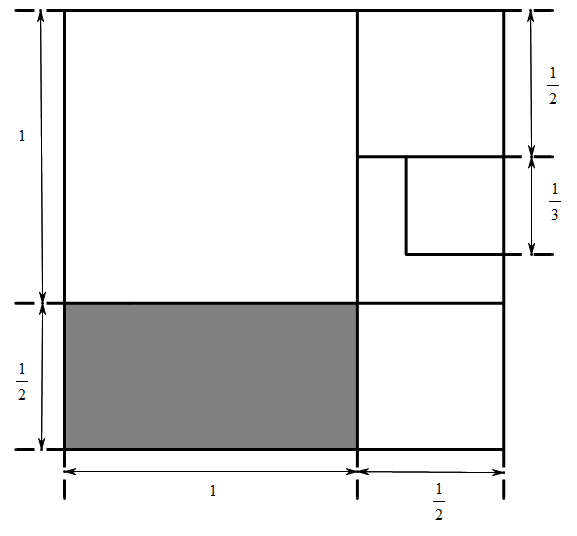
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2