查看数据源：5cd4dd69210b280220ed2b9a
如图所示，设四边形 $ABCD$ 是矩形，点 $E,F$ 分别是线段 $AD,BC$ 的中点，点 $G$ 在线段 $EF$ 上，点 $D,H$ 关于线段 $AG$ 的垂直平分线 $l$ 对称．求证 $\angle HAB=3\angle GAB$．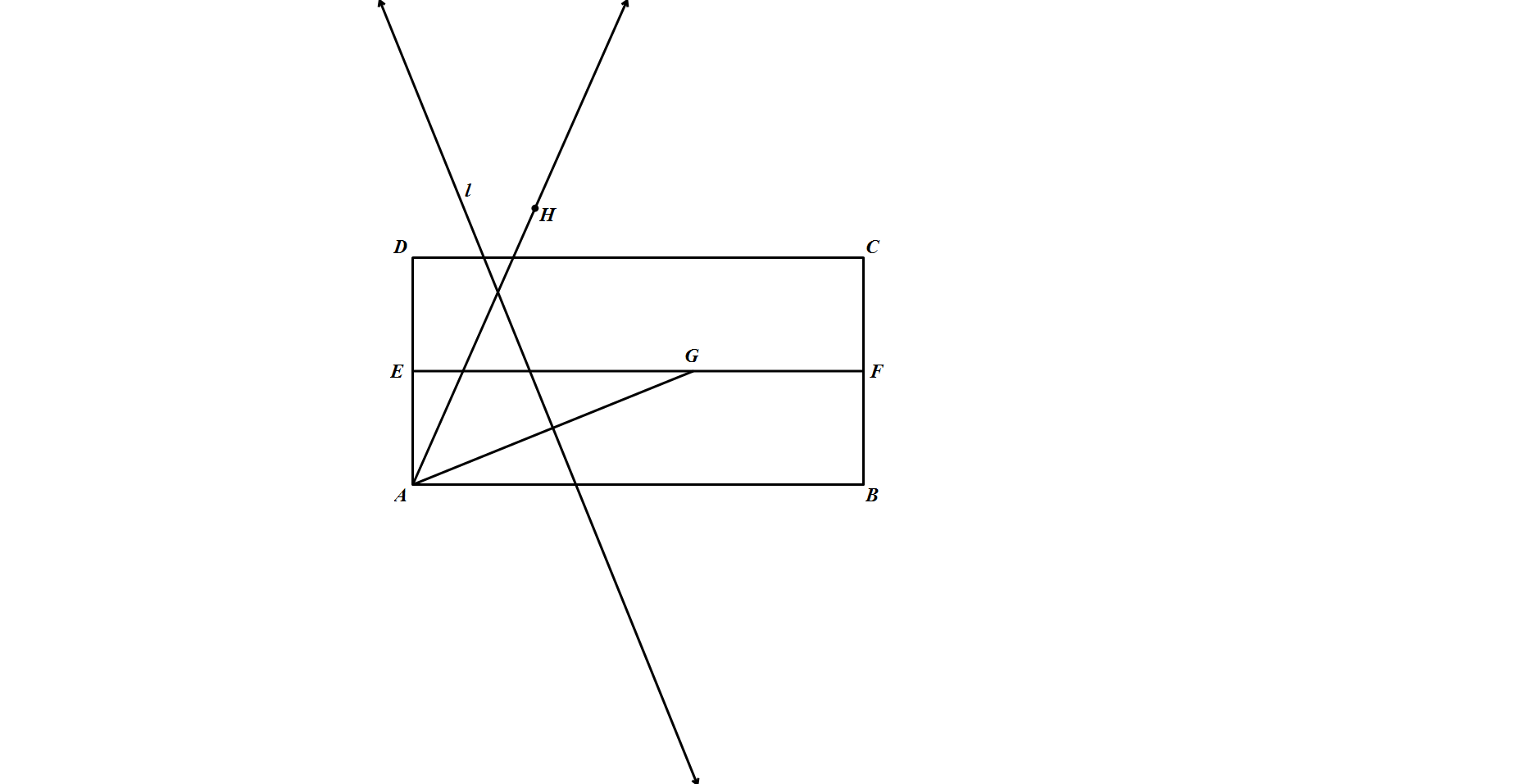
【难度】
【出处】
2018年全国高中数学联赛安徽省预赛
【标注】
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的对称性
  • 知识点
    >
    函数
    >
    函数的图象与性质
    >
    函数的图象变换
【答案】
略
【解析】
由 $E,F$ 分别是 $AD,BC$ 的中点，得 $EF\parallel AB\bot AD$．如图，设 $P$ 是 $E$ 关于 $l$ 的对称点，则 $EP\parallel AG\bot l$，故四边形 $AEPG$ 是等腰梯形．进而 $\angle PAG=\angle EGA=\angle GAB,\angle APG=\angle GEA$，从而 $AP\bot HG$．再由 $HP=DE=EA=PG$，得 $\angle HAP=\angle PAG=\angle GAB$．因此，$\angle HAB=3\angle GAB$．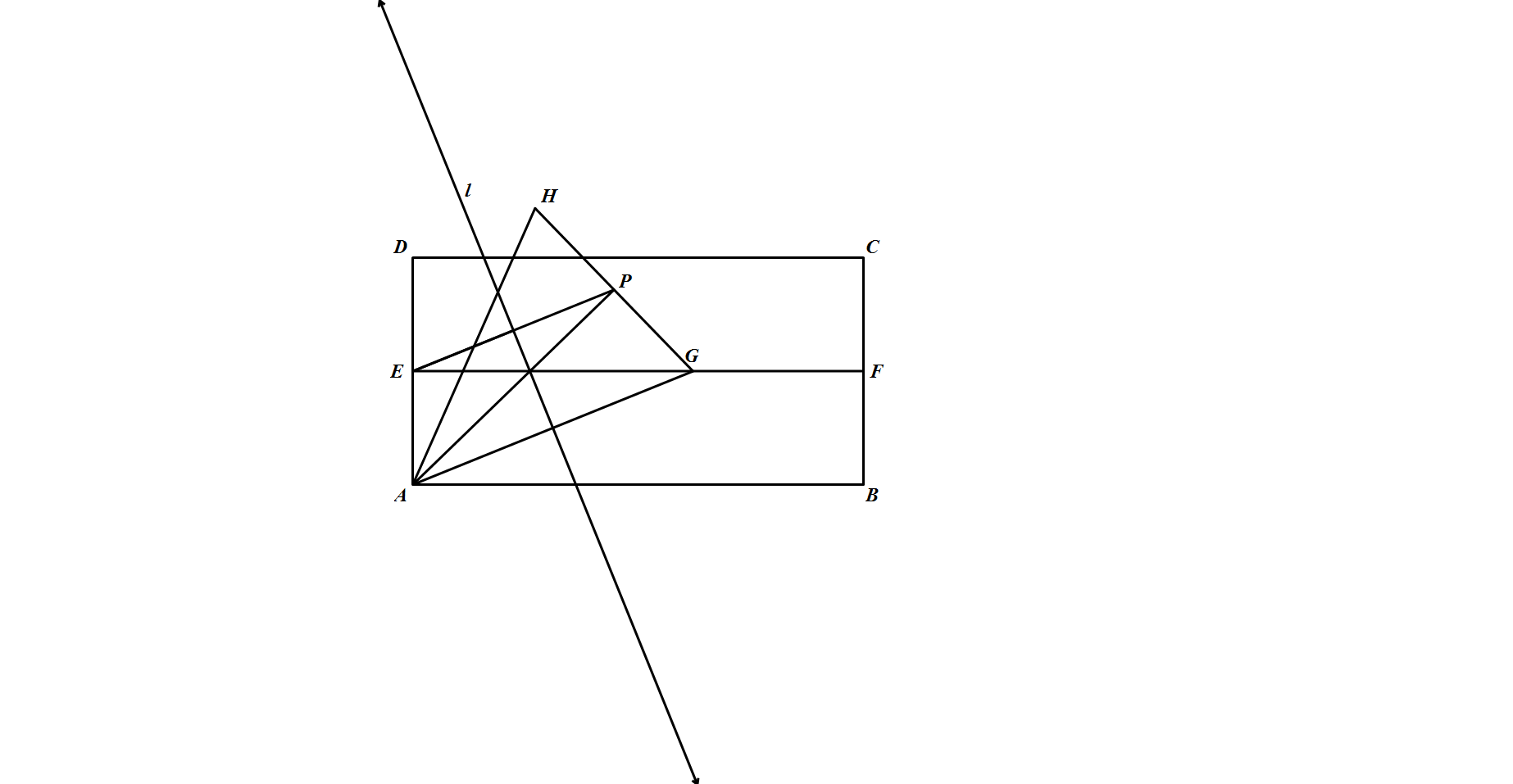
答案 解析 备注
0.109953s