如图 ①,已知矩形 $ABCD$ 满足 $AB=5,AC=\sqrt{34}$,沿平行于 $AD$ 的线段 $EF$ 向上翻折(点 $E$ 在线段 $AB$ 上运动,点 $F$ 在线段 $CD$ 上运动),得到如图 ② 所示的三棱柱 $ABE-DCF$.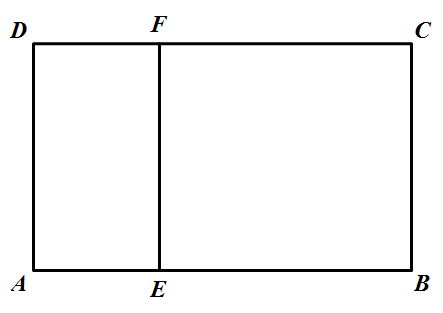 ①
①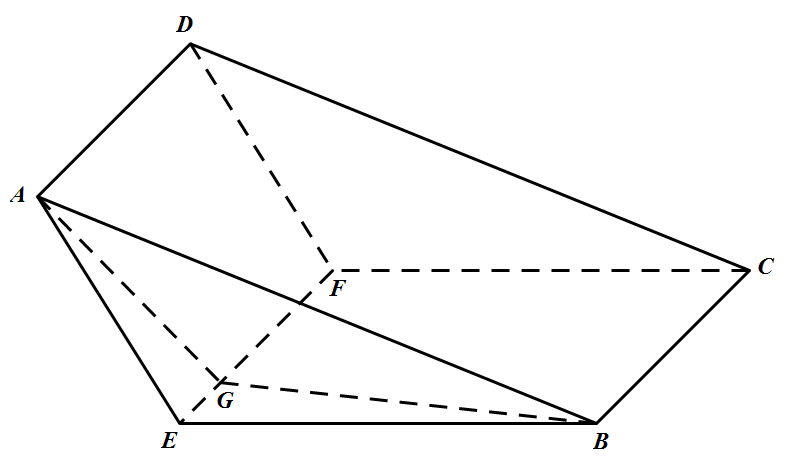 ②
②
 ①
① ②
②【难度】
【出处】
2018年全国高中数学联赛广东省预赛
【标注】
-
若图 ② 中 $\triangle ABG$ 是直角三角形,这里 $G$ 是线段 $EF$ 上的点,试求线段 $EG$ 的长度 $x$ 的取值范围;标注答案$[0,2.5)$解析由题设条件可知 $\triangle AEG,\triangle BEG$ 均为直角三角形,因此 $AG^2=AE^2+x^2,BG^2=BE^2+x^2$.由余弦定理 $AB^2=AE^2+BE^2-2AE\cdot BE\cos\angle AEB$,于是 $2x^2+AE^2+BE^2=AB^2=AE^2+BE^2-2AE\cdot BE\cos\angle AEB,x^2=-AE\cdot BE\cos\angle AEB<AE\cdot BE=t(5-t)=-t^2+5t\leqslant 2.5^2.$ 所以 $x\in[0,2.5)$.又对任意 $k\in[0,2.5),AE=EB=2.5,\angle AEB=\pi-\arccos\dfrac{k^2}{2.5^2}$,则 $x=\sqrt{-AE\cdot BE\cos\angle AEB}=k$,故 $x$ 的取值范围为 $[0,2.5)$.
-
若(1)中 $EG$ 的长度为取值范围内的最大整数,且线段 $AB$ 的长度取得最小值,求二面角 $C-EF-D$ 的值;标注答案$\pi-\arccos\dfrac{8}{25}$解析因为 $AE\bot EF,BE\bot EF$,所以 $\angle AFB$ 就是二面角 $C-EF-D$ 的平面角,又由(1)知 $EG$ 的长度 $x$ 为 $[0,2.5)$ 的最大整数,因此 $x=2$.于是 $AB^2=t^2+(5-t)^2+4=2t^2-10t+29,t\in(0,5)$.因此 $t=2.5$ 时,线段 $AB$ 的长度取得最小值,由此得 $2=-\dfrac{25}{4}\cos\angle AEB,\angle AEB=\pi-\arccos\dfrac{8}{25}$.
-
在(1)与(2)的条件都满足的情况下,求三棱锥 $A-BFG$ 的体积.标注答案$\dfrac{3\sqrt{561}-82}{24}$解析由(1),(2)知 $\angle AEB=\pi-\arccos\dfrac{8}{25}$,$AE=EB=\dfrac{5}{2},AG=BG=\dfrac{\sqrt{41}}{2},EG=2$,且 $EF=\sqrt{AC^2-AB^2}=\sqrt{34-25}=3$.因为 $AE\bot EF,BE\bot EF,AE\bigcap BE=E$,所以 $EF\bot$ 平面 $EAB$,故 ${{V}_{A-BFG}}={{V}_{A-BEF}}-{{V}_{A-BEG}}=\dfrac{1}{3}\left({{S}_{\Delta AEB}}\cdot EF-{{S}_{\Delta AGB}}\cdot EG \right)=\dfrac{1}{3}\left[\dfrac{1}{2}\left( A{{E}^{2}}\sin \angle AEB \right)EF-\dfrac{1}{2}B{{G}^{2}}EG\right]=\\\dfrac{1}{6}\left( \dfrac{25}{4}\sqrt{1-\dfrac{64}{625}}\times 3-\dfrac{41}{4}\times2 \right)=\dfrac{3\sqrt{561}-82}{24}.$
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2
问题3
答案3
解析3
备注3