如图，$\odot O$ 切 $AB,AC$ 于点 $B,C$，过 $C$ 的割线 $CD\parallel AB$ 交 $\odot O$ 于点 $D$，$E$ 是 $AB$ 延长线上一点，直线 $CE$ 分别交 $BD$ 和 $\odot O$ 于点 $F,G$．延长 $BG$ 与 $CD$ 的延长线相交于点 $P$．求证：$A,F,P$ 三点共线．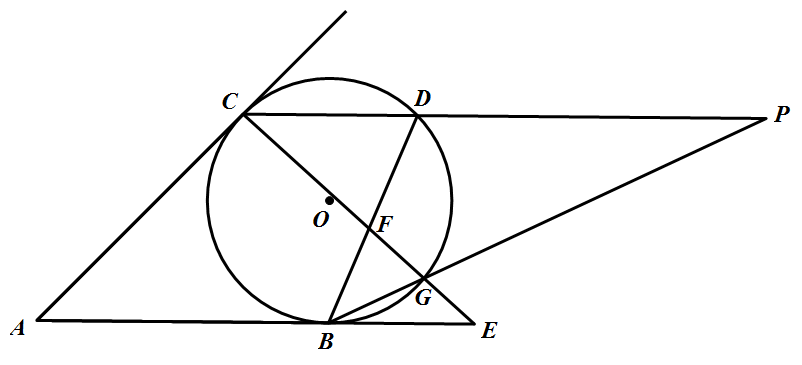
【难度】
【出处】
2018年全国高中数学联赛广西壮族自治区预赛
【标注】
【答案】
略
【解析】
如图，连结 $AF,FP,BC$．由弦切角性质，有 $\angle ABC=\angle ACB=\angle BDC=\angle BCD$．
则 $\triangle ABC$ 与 $\triangle BCD$ 均为等腰三角形且相似．因此可得 $\dfrac{AB}{BC}=\dfrac{BC}{CD}$，于是有 $AB\cdot CD=BC^2$．①
又由 $\angle BDP=\pi-\angle BDC=\angle CBE,\angle DBP=\angle DCG=\angle BEC$，可知 $\triangle BDP\sim\triangle EBC$．则有 $\dfrac{BC}{BE}=\dfrac{DP}{BD}$．从而由 $BC=BD$ 可得 $\dfrac{BC}{BE}=\dfrac{DP}{BC}$，于是 $BC^2=BE\cdot DP$ ②
由 ① 与 ② 可得 $AB\cdot CD=BE\cdot DP$，故 $\dfrac{CD}{BE}=\dfrac{DP}{AB}$．③
由 $CP\parallel AE$ 可知 $\triangle CDF\sim\triangle EBF$，从而 $\dfrac{DF}{FB}=\dfrac{CD}{BE}$．联合 ③ 式，易知 $\dfrac{DF}{FB}=\dfrac{DP}{AB}$．④
由 $CP\parallel AE$ 可得 $\angle FDP=\angle FBA$，从而由 ④ 式可知 $\triangle AFB\sim\triangle PFD,\angle AFB=\angle PFD$，故 $A,F,P$ 三点共线．
则 $\triangle ABC$ 与 $\triangle BCD$ 均为等腰三角形且相似．因此可得 $\dfrac{AB}{BC}=\dfrac{BC}{CD}$，于是有 $AB\cdot CD=BC^2$．①又由 $\angle BDP=\pi-\angle BDC=\angle CBE,\angle DBP=\angle DCG=\angle BEC$，可知 $\triangle BDP\sim\triangle EBC$．则有 $\dfrac{BC}{BE}=\dfrac{DP}{BD}$．从而由 $BC=BD$ 可得 $\dfrac{BC}{BE}=\dfrac{DP}{BC}$，于是 $BC^2=BE\cdot DP$ ②
由 ① 与 ② 可得 $AB\cdot CD=BE\cdot DP$，故 $\dfrac{CD}{BE}=\dfrac{DP}{AB}$．③
由 $CP\parallel AE$ 可知 $\triangle CDF\sim\triangle EBF$，从而 $\dfrac{DF}{FB}=\dfrac{CD}{BE}$．联合 ③ 式，易知 $\dfrac{DF}{FB}=\dfrac{DP}{AB}$．④
由 $CP\parallel AE$ 可得 $\angle FDP=\angle FBA$，从而由 ④ 式可知 $\triangle AFB\sim\triangle PFD,\angle AFB=\angle PFD$，故 $A,F,P$ 三点共线．
答案
解析
备注
