如图，在凸四边形 $ABCD$ 中，$M$ 为边 $AB$ 的中点，且 $MC=MD$．分别过点 $C,D$ 作边 $BC,AD$ 的垂线，设两条垂线的交点为 $P$．过点 $P$ 作 $PQ\bot AB$ 于 $Q$．
求证：$\angle PQC=\angle PQD$．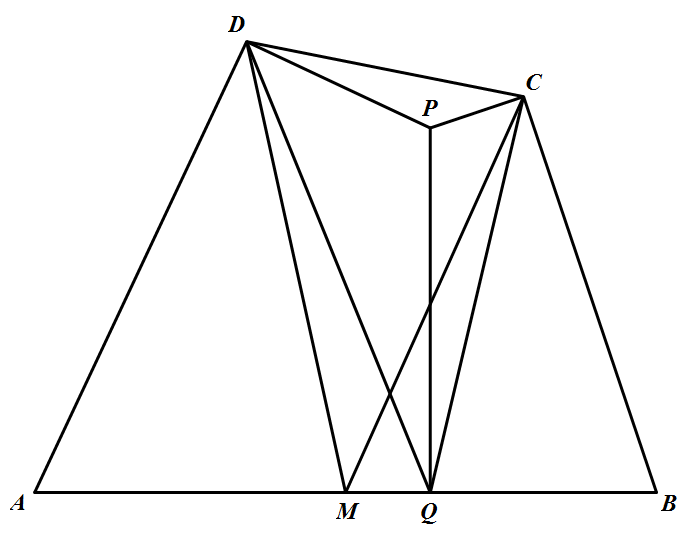
求证：$\angle PQC=\angle PQD$．
【难度】
【出处】
2018年全国高中数学联赛湖南省预赛（A卷）
【标注】
【答案】
略
【解析】
如图，连结 $PA,PB$，分别取 $PA,PB$ 的中点 $E,F$，连结 $EM,ED,FM,FC$，则四边形 $PEMF$ 为平行四边形，从而 $\angle PEM=\angle PFM$．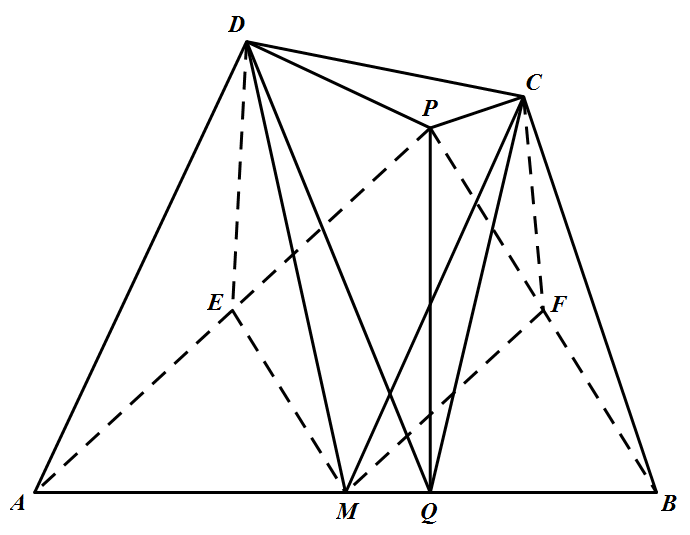
由 $ME=\dfrac{1}{2}BP=CF,MF=\dfrac{1}{2}AP=DE,MD=MC$，所以 $\triangle DEM\cong\triangle MFC$，即 $\triangle DEM=\triangle MFC$．所以 $\angle PED=\angle DEM-\angle PEM=\angle MFC-\angle PFM=\angle PFC$．又 $\angle PED=2\angle PAD,\angle PFC=2\angle PBC$，得 $\angle PAD=\angle PBC$．由于 $\angle PQA=\angle PDA=90^\circ,\angle PQB=\angle PCB=90^\circ$，则 $P,Q,A,D$ 和 $P,Q,B,C$ 分别四点共圆．故 $\angle PQD=\angle PAD,\angle PQC=\angle PBC$，所以 $\angle PQC=\angle PQD$．
由 $ME=\dfrac{1}{2}BP=CF,MF=\dfrac{1}{2}AP=DE,MD=MC$，所以 $\triangle DEM\cong\triangle MFC$，即 $\triangle DEM=\triangle MFC$．所以 $\angle PED=\angle DEM-\angle PEM=\angle MFC-\angle PFM=\angle PFC$．又 $\angle PED=2\angle PAD,\angle PFC=2\angle PBC$，得 $\angle PAD=\angle PBC$．由于 $\angle PQA=\angle PDA=90^\circ,\angle PQB=\angle PCB=90^\circ$，则 $P,Q,A,D$ 和 $P,Q,B,C$ 分别四点共圆．故 $\angle PQD=\angle PAD,\angle PQC=\angle PBC$，所以 $\angle PQC=\angle PQD$．
答案
解析
备注
