如图,四棱锥 $S-ABCD$ 中,$SD\bot $ 底面 $ABCD$,$AB\parallel DC,AD\bot DC,AB=AD=1,DC=SD=2$.$E$ 为棱 $SB$ 上的一点,平面 $EDC\bot $ 平面 $SBC$.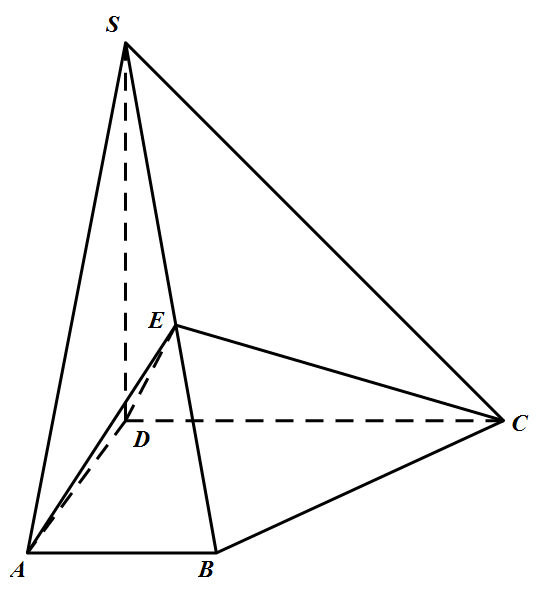

【难度】
【出处】
2018年全国高中数学联赛湖南省预赛(B卷)
【标注】
-
证明:$SE=2EB$;标注答案略解析以 $D$ 为坐标原点,射线 $DA,DC,DS$ 分别为 $x$ 轴,$y$ 轴,$z$ 轴,建立空间直角坐标系 $Dxyz$.设 $A=(1,0,0)$,那么 $B(1,1,0),C(0,2,0),S(0,0,2)$.
$\overrightarrow{SC}=(0,2,-2),\overrightarrow{BC}=(-1,1,0)$.设平面 $SBC$ 的法向量为 $\overrightarrow{n}=(a,b,c)$,由 $\overrightarrow{n}\bot \overrightarrow{SC},\overrightarrow{n}\bot \overrightarrow{BC}$,得到 $\overrightarrow{n}\cdot\overrightarrow{SC}=0,\overrightarrow{n}\cdot\overrightarrow{BC}=0$,所以有 $b-c=0,-a+b=0$,取 $a=b=c=1$,则 $\overrightarrow{n}=(1,1,1)$.又设 $\overrightarrow{SE}=\lambda\overrightarrow{EB}(\lambda>0)$,则 $E\left(\dfrac{\lambda }{1+\lambda },\dfrac{\lambda }{1+\lambda },\dfrac{2}{1+\lambda }\right),\overrightarrow{DE}=\left( \dfrac{\lambda }{1+\lambda },\dfrac{\lambda}{1+\lambda },\dfrac{2}{1+\lambda } \right),\overrightarrow{DC}=\left( 0,2,0\right)$.
设平面 $CDE$ 的法向量为 $\overrightarrow{m}=(x,y,z)$,由 $\overrightarrow{m}\bot \overrightarrow{DE},\overrightarrow{m}\bot\overrightarrow{DC}$,得到 $\overrightarrow{m}\cdot\overrightarrow{DE}=0,\overrightarrow{m}\cdot\overrightarrow{DC}=0$,故 $\dfrac{\lambda x}{1+\lambda}+\dfrac{\lambda y}{1+\lambda}+\dfrac{2z}{1+\lambda}=0,2y=0$.令 $x=2$,则 $\overrightarrow{m}=(2,0,-\lambda)$,由平面 $DEC\bot $ 平面 $SBC$,得到 $\overrightarrow{m}\bot\overrightarrow{n}$,所以 $\overrightarrow{m}\cdot\overrightarrow{n}=0,2-\lambda=0,\lambda=2$,故 $SE=2EB$. -
求二面角 $A-DE-C$ 的大小.标注答案$120^\circ$解析由(1)知 $\overrightarrow{DE}=(\dfrac{2}{3},\dfrac{2}{3},\dfrac{2}{3})$,取 $DE$ 的中点 $F$,则 $F=(\dfrac{1}{3},\dfrac{1}{3},\dfrac{1}{3}),\overrightarrow{FA}=(\dfrac{2}{3},-\dfrac{1}{3},-\dfrac{1}{3})$,故 $\overrightarrow{FA}\cdot\overrightarrow{DE}=0,\overrightarrow{FA}\bot\overrightarrow{DE}$.又 $\overrightarrow{EC}=(-\dfrac{2}{3},\dfrac{4}{3},-\dfrac{2}{3})$,故 $\overrightarrow{EC}\bot\overrightarrow{DE}$,因此向量 $\overrightarrow{FA}$ 与 $\overrightarrow{EC}$ 的夹角等于二面角 $A-DE-C$ 的平面角,于是 $\cos(\overrightarrow{FA},\overrightarrow{EC})=\dfrac{\overrightarrow{FA}\cdot\overrightarrow{EC}}{|\overrightarrow{FA}||\overrightarrow{EC}|}=-\dfrac{1}{2}$,所以二面角 $A-DE-C$ 的大小为 $120^\circ$.
题目
问题1
答案1
解析1
备注1
问题2
答案2
解析2
备注2