已知 $P$ 是矩形 $ABCD$ 所在平面上的一点,则有 $PA^2+PC^2=PB^2+PD^2$.试证明该命题.
【难度】
【出处】
2018年全国高中数学联赛湖南省预赛(B卷)
【标注】
【答案】
略
【解析】
如图 ①,设在直角坐标平面中,矩形 $ABCD$ 的顶点坐标分别为 $A(-a,-b),B(a,-b),C(a,b),D(-a,b)$.点 $P(x,y)$ 是直角坐标平面上任意一点,则 $P{{A}^{2}}+P{{C}^{2}}={{\left(x+a \right)}^{2}}+{{\left( y+b \right)}^{2}}+{{\left( x-a\right)}^{2}}+{{\left( y-b \right)}^{2}}=2\left({{x}^{2}}+{{y}^{2}}+{{a}^{2}}+{{b}^{2}} \right),\\P{{B}^{2}}+P{{D}^{2}}={{\left(x-a \right)}^{2}}+{{\left( y+b \right)}^{2}}+{{\left( x+a\right)}^{2}}+{{\left( y-b \right)}^{2}}=2\left({{x}^{2}}+{{y}^{2}}+{{a}^{2}}+{{b}^{2}} \right).$
故 $PA^2+PC^2=PB^2+PD^2$.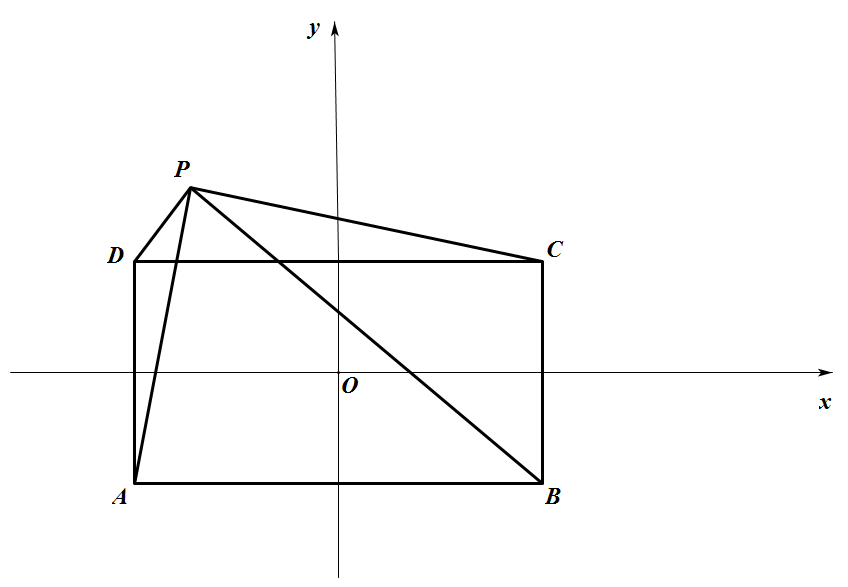
故 $PA^2+PC^2=PB^2+PD^2$.

答案
解析
备注