如图,在平面直角坐标系 $xOy$ 中,已知圆 $O$ 的方程为 $x^2+y^2=4$,过点 $P(0,1)$ 的直线 $l$ 与圆 $O$ 交于点 $A,B$,与 $x$ 轴交于点 $Q$.设 $\overrightarrow{QA}=\lambda\overrightarrow{PA},\overrightarrow{OB}=\mu\overrightarrow{PB}$,求证:$\lambda+\mu$ 为定值.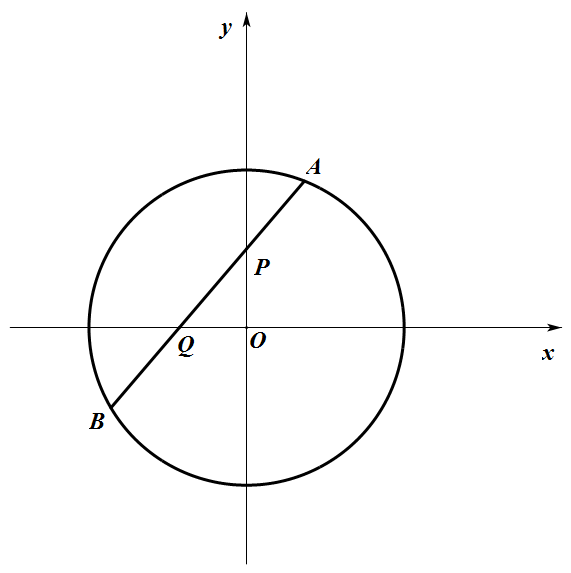

【难度】
【出处】
2018年全国高中数学联赛江苏省预赛(初赛试题)
【标注】
【答案】
$\dfrac{8}{3}$
【解析】
当 $AB$ 与 $x$ 轴垂直时,此时点 $Q$ 与点 $O$ 重合从而 $\lambda =2,\mu =\dfrac{2}{3},\lambda+\mu=\dfrac{8}{3}$.当点 $Q$ 与点 $O$ 不重合时,直线 $AB$ 的斜率存在.设 $AB:y=kx+1,A(x_1,y_1),B(x_2,y_2)$,则 $Q(-\dfrac{1}{k},0)$.由题设得:$x_1+\dfrac{1}{k}=\lambda x_1,x_2+\dfrac{1}{k}=\mu x_2$,即 $\lambda + \mu=1+\dfrac{1}{kx_1}+1+\dfrac{1}{kx_2}=2+\dfrac{x_1+x_2}{kx_1x_2}$.将 $y=kx+1$ 代入 $x^2+y^2=4$,得 $(1+k^2)x^2+2kx-3=0$,则 $\Delta>0,x_1+x_2=\dfrac{-2k}{1+k^2},x_1x_2=\dfrac{-3}{1+k^2}$.所以 $\lambda +\mu =2+\dfrac{-2k}{-3k}=\dfrac{8}{3}$.
综上,$\lambda+\mu$ 为定值 $\dfrac{8}{3}.$
综上,$\lambda+\mu$ 为定值 $\dfrac{8}{3}.$
答案
解析
备注