如图,在圆内接四边形 $ABCD$ 中,对角线 $AC$ 与 $BD$ 交于点 $P$,$\triangle ABD$ 与 $\triangle ABC$ 的内心分别为 $I_1$ 和 $I_2$,直线 $I_1I_2$ 分别与 $AC,BD$ 交于点 $M,N$,求证:$PM=PN$.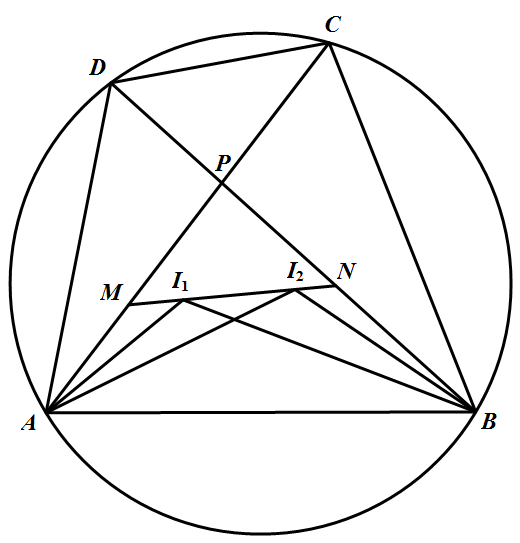

【难度】
【出处】
2018年全国高中数学联赛江苏省预赛(初赛试题)
【标注】
【答案】
略
【解析】
如图,因为 $I_1,I_2$ 分别为 $\triangle ABD$ 与 $\triangle ABC$ 的内心,所以 $\angle I_1AB=\dfrac{1}{2}\angle DAB,\angle I_1AB=\dfrac{1}{2}\angle DAB,\angle I_2BA=\dfrac{1}{2}\angle CAB,\angle I_2BA=\dfrac{1}{2}\angle CAB,$ 故 $\angle AI_1B=180^\circ-\dfrac{1}{2}(\angle DAB+\angle DBA),\angle AI_2B=180^\circ-\dfrac{1}{2}(\angle CAB+\angle CBA)$.在 $\triangle ABD$ 与 $\triangle ABC$ 中,$\angle ADB=\angle ACB$,所以 $\angle DAB+\angle DAB=\angle CAB+\angle CBA$,从而 $\angle AI_1B=\angle AI_2B$,故 $A,I_1,I_2,B$ 四点共圆.因此 $\angle I_1I_2A=\angle I_1BA=\dfrac{1}{2}\angle DBA$,则 $\angle PMN=\angle MAI_2+\angle MI_2A=\dfrac{1}{2}(\angle CAB+\angle DBA).$ 同理,$\angle PNM=\dfrac{1}{2}(\angle CAB+\angle DBA).$ 所以 $\angle PMN=\angle PNM$,即 $PM=PN$.
答案
解析
备注