设 $a,b$ 是实数,并且对任意 $x\in[0,1]$,恒有 $|ax+b-\sqrt{1-x^2}|\leqslant\dfrac{\sqrt{2}-1}{2}$,求 $a,b$ 的值.
【难度】
【出处】
2018年全国高中数学联赛江苏省预赛(复赛加试)
【标注】
【答案】
$a=-1,b=\dfrac{1}{2}(\sqrt{2}+1)$
【解析】
不等式 $|ax+b-\sqrt{1-x^2}|\leqslant \dfrac{\sqrt{2}-1}{2}$ 等价于 $\sqrt{1-x^2}-\dfrac{1}{2}(\sqrt{2}-1)\leqslant ax+b\leqslant \sqrt{1-x^2}+\dfrac{1}{2}(\sqrt{2}-1)$.令 $y_1=ac+b$,①
$y_2=\sqrt{1-x^2}+\dfrac{1}{2}(\sqrt{2}-1)$ ②
$y_3=\sqrt{1-x^2}-\dfrac{1}{2}(\sqrt{2}-1)$ ③
在 $[0,1]$ 中,① 式表示 $x=0$ 与 $x=1$ 之间的一条线段,②,③ 分别表示以 $C(0,\dfrac{1}{2}(\sqrt{2}-1))$ 和 $D(0,-\dfrac{1}{2}(\sqrt{2}-1))$ 为圆心.$1$ 为半径的右上 $dfrac{1}{4}$ 圆周.设 $y_2=\sqrt{1-x^2}+\dfrac{1}{2}(\sqrt{2}-1)$ 在 $[0,1]$ 中的两端点分别为 $A,B$,则 $A,B$ 的坐标分别为 $(0,\dfrac{1}{2}(\sqrt{2}+1)),(1,\dfrac{1}{2}(\sqrt{2}-1))$.
因此直线 $AB$ 的方程为 $y=-x+\dfrac{1}{2}(\sqrt{2}+1)$,而点 $D(0,-\dfrac{1}{2}(\sqrt{2}-1))$ 到直线 $AB$ 的距离为 $1$,所以线段 $AB$ 与四分之一圆周相切(如图).由此可见,对任意 $x\in[0,1]$,使 $y_3\leqslant y_1\leqslant y_2$ 恒成立的唯一线段是 $y=-x+\dfrac{1}{2}(\sqrt{2}+1),x\in[0,1]$.所以 $a=-1,b=\dfrac{1}{2}(\sqrt{2}+1)$.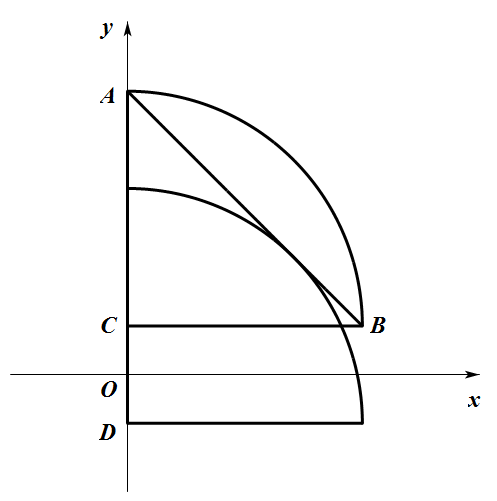
$y_2=\sqrt{1-x^2}+\dfrac{1}{2}(\sqrt{2}-1)$ ②
$y_3=\sqrt{1-x^2}-\dfrac{1}{2}(\sqrt{2}-1)$ ③
在 $[0,1]$ 中,① 式表示 $x=0$ 与 $x=1$ 之间的一条线段,②,③ 分别表示以 $C(0,\dfrac{1}{2}(\sqrt{2}-1))$ 和 $D(0,-\dfrac{1}{2}(\sqrt{2}-1))$ 为圆心.$1$ 为半径的右上 $dfrac{1}{4}$ 圆周.设 $y_2=\sqrt{1-x^2}+\dfrac{1}{2}(\sqrt{2}-1)$ 在 $[0,1]$ 中的两端点分别为 $A,B$,则 $A,B$ 的坐标分别为 $(0,\dfrac{1}{2}(\sqrt{2}+1)),(1,\dfrac{1}{2}(\sqrt{2}-1))$.
因此直线 $AB$ 的方程为 $y=-x+\dfrac{1}{2}(\sqrt{2}+1)$,而点 $D(0,-\dfrac{1}{2}(\sqrt{2}-1))$ 到直线 $AB$ 的距离为 $1$,所以线段 $AB$ 与四分之一圆周相切(如图).由此可见,对任意 $x\in[0,1]$,使 $y_3\leqslant y_1\leqslant y_2$ 恒成立的唯一线段是 $y=-x+\dfrac{1}{2}(\sqrt{2}+1),x\in[0,1]$.所以 $a=-1,b=\dfrac{1}{2}(\sqrt{2}+1)$.
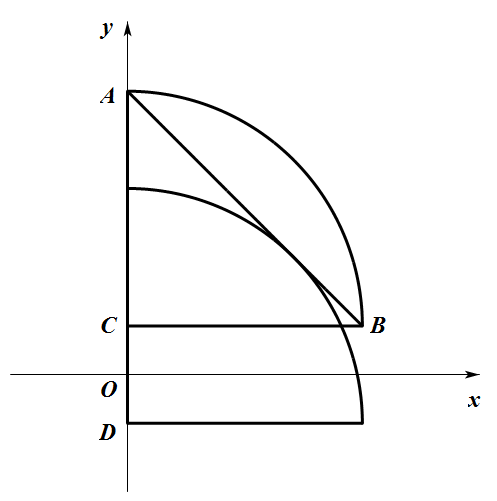
答案
解析
备注