如图,大圆和小圆为同心圆,其圆心为 $O$.过大圆上一点 $A$ 作小圆的切线 $AC$,切点为 $B$,点 $C$ 在大圆上,$D$ 为 $AB$ 的中点.$\triangle ACE$ 的顶点 $E$ 在小圆上,$AE$ 交小圆于 $F$.设 $CE,DF$ 的垂直平分线的交点 $P$ 在直线 $AC$ 上.求证:$CF\bot DF$.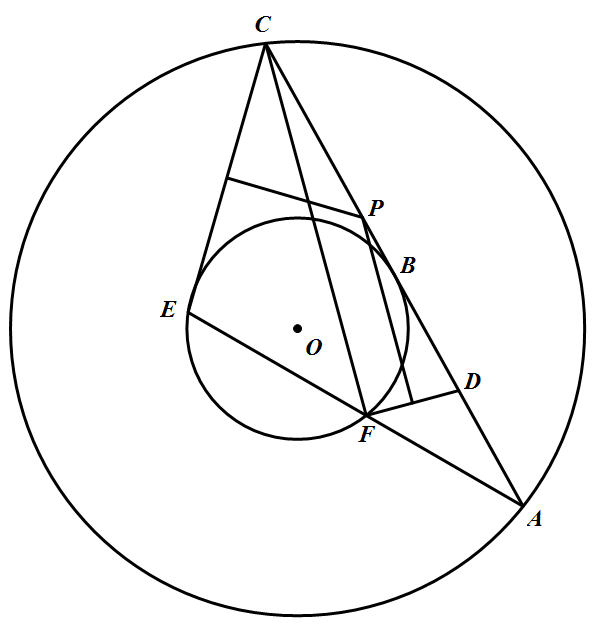

【难度】
【出处】
2018年全国高中数学联赛江苏省预赛(复赛加试)
【标注】
【答案】
略
【解析】
连结 $OB,PE,PF$.由 $AC$ 是小圆的切线,得 $OB\bot AC$.又 $AC$ 是大圆的弦,所以 $AB=BC$.由切割线定理得 $AB^2=AF\cdot AE$ ①
又由 $D$ 为 $AB$ 的中点,可得 $AB=2AD$,又 $AB=\dfrac{1}{2}AC$,代入 ① 得 $AD\cdot AC=AF\cdot AE$,则 $D,F,E,C$ 四点共圆.由点 $P$ 是 $CE,DF$ 的垂直平分线,故 $PE=PC,PF=PD$.②
从而 $\angle PEC=\angle PCE,\angle PFD=\angle PDF$.③
由 $D,F,E,C$ 四点共圆得
$\angle PEF=180^\circ-(\angle PEC+\angle PDF),\angle PFE=180^\circ-(\angle PFD+\angle PCE).$ 又由 ③ 可得 $\angle PEF=\angle PFE$,则 $PE=PF$.又由 ② 可得,$PC=PD=PF$.故 $CF\bot DF$.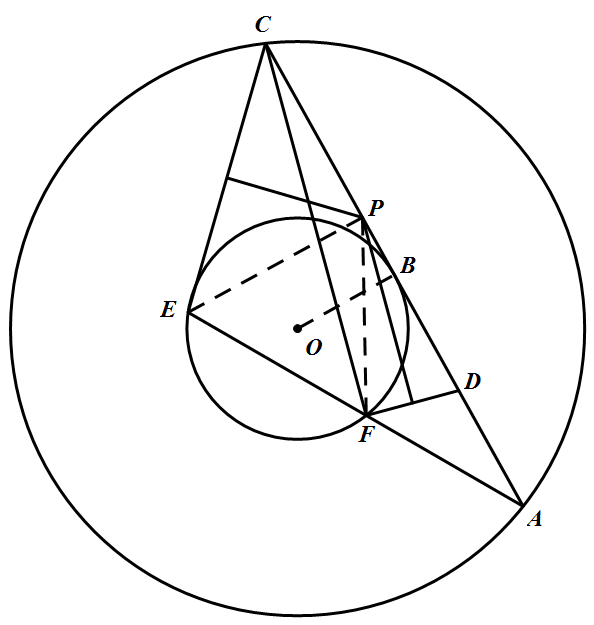
又由 $D$ 为 $AB$ 的中点,可得 $AB=2AD$,又 $AB=\dfrac{1}{2}AC$,代入 ① 得 $AD\cdot AC=AF\cdot AE$,则 $D,F,E,C$ 四点共圆.由点 $P$ 是 $CE,DF$ 的垂直平分线,故 $PE=PC,PF=PD$.②
从而 $\angle PEC=\angle PCE,\angle PFD=\angle PDF$.③
由 $D,F,E,C$ 四点共圆得
$\angle PEF=180^\circ-(\angle PEC+\angle PDF),\angle PFE=180^\circ-(\angle PFD+\angle PCE).$ 又由 ③ 可得 $\angle PEF=\angle PFE$,则 $PE=PF$.又由 ② 可得,$PC=PD=PF$.故 $CF\bot DF$.

答案
解析
备注