如图所示,在平面直角坐标系 $xOy$ 中,$A,B$ 与 $C,D$ 分别是椭圆 $\Gamma:\dfrac{x^2}{a^2}+\dfrac{y^2}{b^2}=1(a>b>0)$ 的左右顶点与上下顶点.设 $P,Q$ 是 $\Gamma$ 上且位于第一象限的两点,满足 $OQ\parallel AP$,$M$ 是线段 $AP$ 的中点,射线 $OM$ 与椭圆交于点 $R$.
证明:线段 $OQ,OR,BC$ 能构成一个直角三角形.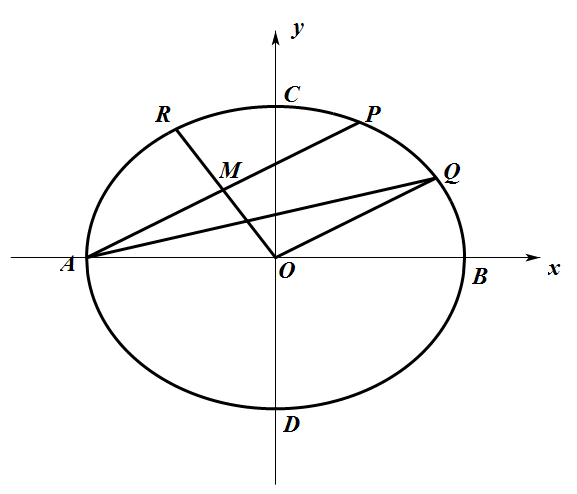
证明:线段 $OQ,OR,BC$ 能构成一个直角三角形.

【难度】
【出处】
2018年全国高中数学联赛(B卷一试试题)
【标注】
【答案】
略
【解析】
设点 $P$ 坐标为 $(x_0,y_0)$.由于 $\overrightarrow{OQ}\parallel \overrightarrow{AP},\overrightarrow{AP}=\overrightarrow{OP}-\overrightarrow{OA};\overrightarrow{OR}\parallel\overrightarrow{OM},\overrightarrow{OM}=\dfrac{1}{2}(\overrightarrow{OP}+\overrightarrow{OA})$,故存在实数 $\lambda,\mu$,使得 $\overrightarrow{OQ}=\lambda(\overrightarrow{OP}-\overrightarrow{OA}),\overrightarrow{OR}=\mu(\overrightarrow{OP}+\overrightarrow{OA})$.此时点 $Q,R$ 的坐标可分别表示是 $(\lambda(x_0+a),\lambda y_0),(\mu(x_0-a),\mu y_0)$.由于点 $Q,R$ 都在椭圆上,所以 ${{\lambda}^{2}}\left( \dfrac{{{\left( {{x}_{0}}+a \right)}^{2}}}{{{a}^{2}}}+\dfrac{y_{0}^{2}}{{{b}^{2}}}\right)={{\mu }^{2}}\left( \dfrac{{{\left( {{x}_{0}}-a \right)}^{2}}}{{{a}^{2}}}+\dfrac{y_{0}^{2}}{{{b}^{2}}}\right)=1$.
结合 $\dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}=1$ 知,上式可化为 $\lambda^2(2+\dfrac{2x_0}{a})=\mu^2(2-\dfrac{2x_0}{a})=1$,解得 $\lambda^2=\dfrac{a}{2(a+x_0)},\mu^2=\dfrac{a}{2(a-x_0)}$.
因此 ${{\left|OQ \right|}^{2}}+{{\left| OR \right|}^{2}}={{\lambda }^{2}}\left( {{\left({{x}_{0}}+a \right)}^{2}}+y_{0}^{2} \right)+{{\mu }^{2}}\left( {{\left({{x}_{0}}-a \right)}^{2}}+y_{0}^{2} \right)\\=\dfrac{a}{2\left( a+{{x}_{0}}\right)}\left( {{\left( {{x}_{0}}+a \right)}^{2}}+y_{0}^{2} \right)+\dfrac{a}{2\left(a-{{x}_{0}} \right)}\left( {{\left( {{x}_{0}}-a \right)}^{2}}+y_{0}^{2}\right)\\=\dfrac{a\left( a+{{x}_{0}} \right)}{2}+\dfrac{ay_{0}^{2}}{2\left(a+{{x}_{0}} \right)}+\dfrac{a\left( a-{{x}_{0}} \right)}{2}+\dfrac{ay_{0}^{2}}{2\left(a-{{x}_{0}} \right)}\\={{a}^{2}}+\dfrac{ay_{0}^{2}}{2}\left( \dfrac{1}{a+{{x}_{0}}}+\dfrac{1}{a-{{x}_{0}}}\right)\\={{a}^{2}}+\dfrac{ay_{0}^{2}}{2}\cdot \dfrac{2a}{{{a}^{2}}-x_{0}^{2}}={{a}^{2}}+\dfrac{{{a}^{2}}\cdot{{b}^{2}}\left( 1-\dfrac{x_{0}^{2}}{{{a}^{2}}}\right)}{{{a}^{2}}-x_{0}^{2}}={{a}^{2}}+{{b}^{2}}={{\left| BC \right|}^{2}}.$
从而线段 $OQ,OR,BC$ 能构成一个直角三角形.
结合 $\dfrac{x_0^2}{a^2}+\dfrac{y_0^2}{b^2}=1$ 知,上式可化为 $\lambda^2(2+\dfrac{2x_0}{a})=\mu^2(2-\dfrac{2x_0}{a})=1$,解得 $\lambda^2=\dfrac{a}{2(a+x_0)},\mu^2=\dfrac{a}{2(a-x_0)}$.
因此 ${{\left|OQ \right|}^{2}}+{{\left| OR \right|}^{2}}={{\lambda }^{2}}\left( {{\left({{x}_{0}}+a \right)}^{2}}+y_{0}^{2} \right)+{{\mu }^{2}}\left( {{\left({{x}_{0}}-a \right)}^{2}}+y_{0}^{2} \right)\\=\dfrac{a}{2\left( a+{{x}_{0}}\right)}\left( {{\left( {{x}_{0}}+a \right)}^{2}}+y_{0}^{2} \right)+\dfrac{a}{2\left(a-{{x}_{0}} \right)}\left( {{\left( {{x}_{0}}-a \right)}^{2}}+y_{0}^{2}\right)\\=\dfrac{a\left( a+{{x}_{0}} \right)}{2}+\dfrac{ay_{0}^{2}}{2\left(a+{{x}_{0}} \right)}+\dfrac{a\left( a-{{x}_{0}} \right)}{2}+\dfrac{ay_{0}^{2}}{2\left(a-{{x}_{0}} \right)}\\={{a}^{2}}+\dfrac{ay_{0}^{2}}{2}\left( \dfrac{1}{a+{{x}_{0}}}+\dfrac{1}{a-{{x}_{0}}}\right)\\={{a}^{2}}+\dfrac{ay_{0}^{2}}{2}\cdot \dfrac{2a}{{{a}^{2}}-x_{0}^{2}}={{a}^{2}}+\dfrac{{{a}^{2}}\cdot{{b}^{2}}\left( 1-\dfrac{x_{0}^{2}}{{{a}^{2}}}\right)}{{{a}^{2}}-x_{0}^{2}}={{a}^{2}}+{{b}^{2}}={{\left| BC \right|}^{2}}.$
从而线段 $OQ,OR,BC$ 能构成一个直角三角形.
答案
解析
备注