如图，$\triangle ABC$ 为锐角三角形，$AB<AC$，$M$ 为 $BC$ 边的中点，点 $D$ 和 $E$ 分别为 $\triangle ABC$ 的外接圆 $\overparen{BAC}$ 和 $\overparen{BC}$ 的中点，$F$ 为 $\triangle ABC$ 的内切圆在 $AB$ 边上的切点，$G$ 为 $AE$ 与 $BC$ 的交点，$N$ 在线段 $EF$ 上，满足 $NB\bot AB$．
证明：若 $BN=EM$，则 $DF\bot FG$．（答题时请将图画在答卷纸上）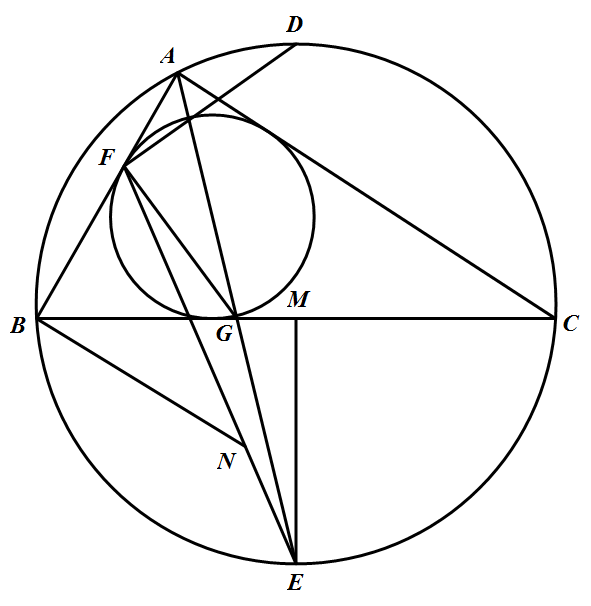
证明：若 $BN=EM$，则 $DF\bot FG$．（答题时请将图画在答卷纸上）
【难度】
【出处】
2018年全国高中数学联赛（A卷加试试题）
【标注】
【答案】
略
【解析】
由条件知，$DE$ 为 $\triangle ABC$ 外接圆的直径，$DE\bot BC$ 于 $M$，$AE\bot AD$．记 $I$ 为 $\triangle ABC$ 的内心，则 $I$ 在 $AE$ 上，$IF\bot AB$．由 $NB\bot AB$ 可知 $\angle NBE=\angle ABE-\angle ABN=(180 ^\circ-\angle ADE)-90^\circ=90^\circ-\angle ADE=\angle MEI$．①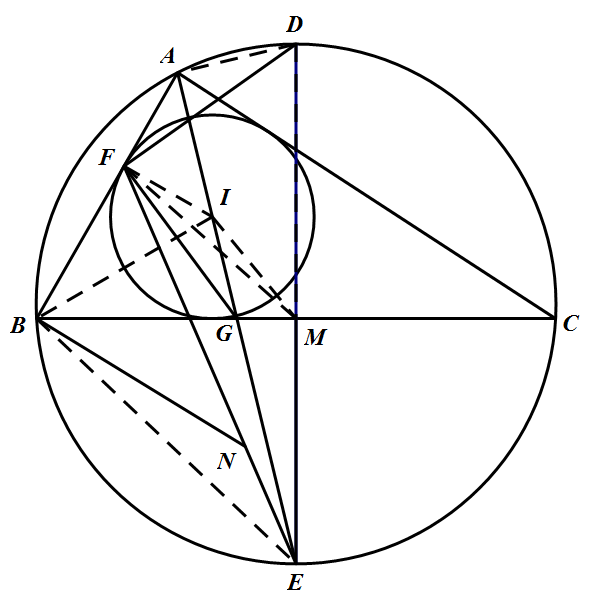
又根据内心的性质，有 $\angle EBI=\angle EBC+\angle CBI=\angle EAC+\angle ABI=\angle EAB+\angle ABI=\angle EIB$，从而 $BE=EI$．结合 $BN=EM$ 及 ① 知，$\triangle NBE\cong\triangle MEI$．于是 $\angle EMI=\angle BNE=90^\circ+\angle BFE=180^\circ-\angle EFI$，故 $E,F,I,M$ 四点共圆．进而可知 $\angle AFM=90^\circ+\angle IFM=90^\circ+\angle IEM=\angle AGM$，从而 $A,F,G,M$ 四点共圆．再由 $\angle DAG=\angle DMG=90^\circ$ 知，$A,G,M,D$ 四点共圆，所以 $A,F,G,M,D$ 五点共圆．从而 $\angle DFG=\angle DAG=90^\circ$，即 $DF\bot FG$．
又根据内心的性质，有 $\angle EBI=\angle EBC+\angle CBI=\angle EAC+\angle ABI=\angle EAB+\angle ABI=\angle EIB$，从而 $BE=EI$．结合 $BN=EM$ 及 ① 知，$\triangle NBE\cong\triangle MEI$．于是 $\angle EMI=\angle BNE=90^\circ+\angle BFE=180^\circ-\angle EFI$，故 $E,F,I,M$ 四点共圆．进而可知 $\angle AFM=90^\circ+\angle IFM=90^\circ+\angle IEM=\angle AGM$，从而 $A,F,G,M$ 四点共圆．再由 $\angle DAG=\angle DMG=90^\circ$ 知，$A,G,M,D$ 四点共圆，所以 $A,F,G,M,D$ 五点共圆．从而 $\angle DFG=\angle DAG=90^\circ$，即 $DF\bot FG$．
答案
解析
备注
