如图所示,在等腰 $\triangle ABC$ 中,$AB=AC$,边 $AC$ 上一点 $D$ 及 $BC$ 延长线上一点 $E$ 满足 $\dfrac{AD}{DC}=\dfrac{BC}{2CE}$,以 $AB$ 为直径的圆 $w$ 与线段 $DE$ 交于一点 $F$.证明:$B,C,F,D$ 四点共圆.(答题时请将图画在答卷纸上)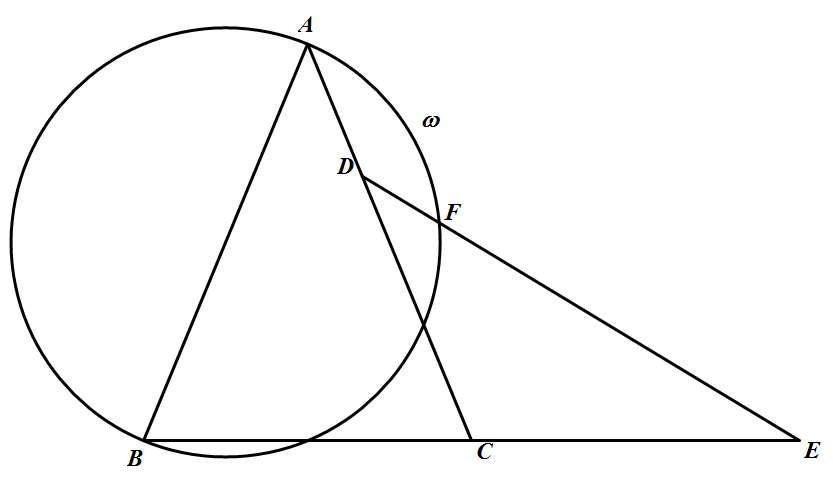

【难度】
【出处】
2018年全国高中数学联赛(B卷加试试题)
【标注】
【答案】
略
【解析】
如图,取 $BC$ 中点 $H$,则由 $AB=AC$ 知 $AH\bot BC$,故 $H$ 在圆 $w$ 上.
延长 $FD$ 至 $G$,使得 $AG\parallel BC$,结合已知条件得,$\dfrac{AG}{CE}=\dfrac{AD}{DC}=\dfrac{BC}{2CE}$,故 $AG=\dfrac{1}{2}BC=BH=HC$,从而 $AGBH$ 为矩形,$AGHC$ 为平行四边形.由 $AGBH$ 为矩形知,$G$ 亦在圆 $w$ 上.故 $\angle HGF=\angle HBF$.又 $AGHC$ 为平行四边形,由 $AC\parallel GH$,得 $\angle CDF=\angle HGF$.所以 $\angle CDF=\angle HBF=\angle CBF$,故 $B,C,F,D$ 四点共圆.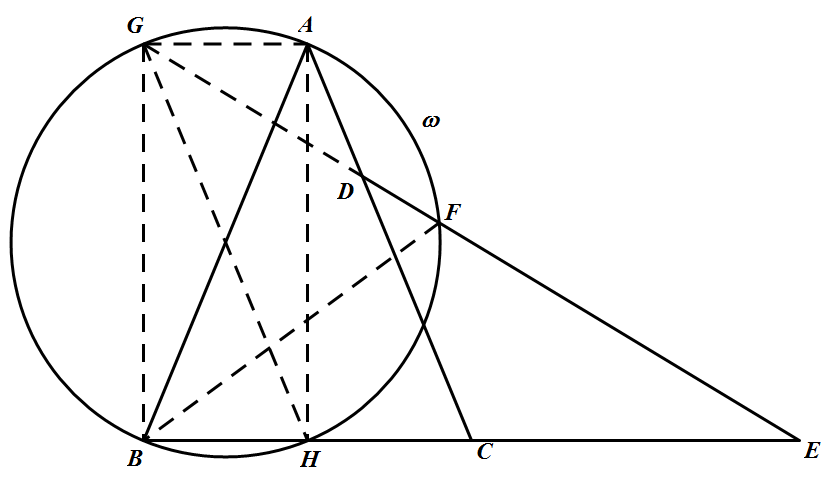
延长 $FD$ 至 $G$,使得 $AG\parallel BC$,结合已知条件得,$\dfrac{AG}{CE}=\dfrac{AD}{DC}=\dfrac{BC}{2CE}$,故 $AG=\dfrac{1}{2}BC=BH=HC$,从而 $AGBH$ 为矩形,$AGHC$ 为平行四边形.由 $AGBH$ 为矩形知,$G$ 亦在圆 $w$ 上.故 $\angle HGF=\angle HBF$.又 $AGHC$ 为平行四边形,由 $AC\parallel GH$,得 $\angle CDF=\angle HGF$.所以 $\angle CDF=\angle HBF=\angle CBF$,故 $B,C,F,D$ 四点共圆.

答案
解析
备注