已知四边形 $P_1P_2P_3P_4$ 的四个顶点位于 $\triangle ABC$ 的边上，求证：四个三角形 $\triangle P_{1} P_{2} P_{3}, \triangle P_{1} P_{2} P_{4}, \triangle P_{1} P_{3} P_{4},\triangle P_{2} P_{3} P_{4}$ 中，至少有一个的面积不大于 $\triangle ABC$ 面积的四分之一．
【难度】
【出处】
1986第1届CMO试题
【标注】
【答案】
略
【解析】
为方便起见，我们直接用 $\triangle ABC$ 来代表 $\triangle ABC$ 的面积，其余类似的记号，均有此含义．
要考虑两种情况：
（1）$\triangle ABC$ 中，有一边上不含 $P_{1}, P_{2}, P_{3}, P_{4}$ 中的任何一点，如图所示；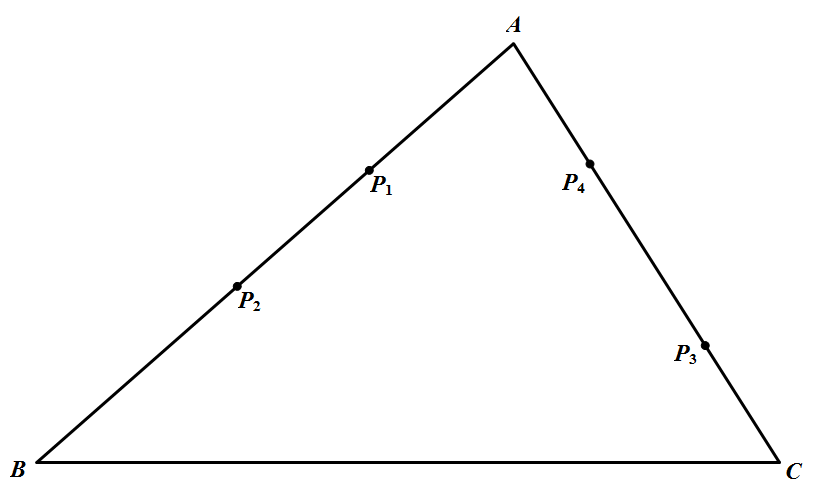
（2）$\triangle ABC$ 的每一条边上均有 $P_{1}, P_{2}, P_{3}, P_{4}$ 中的点，当然至少有一条边，例如 $BC$ 边上，含有其中的两个点，如图所示．
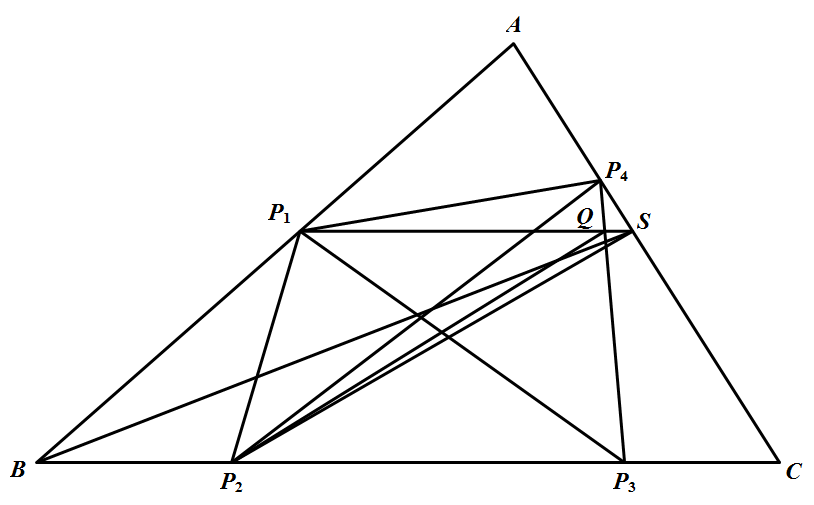先讨论后一种情形．设 $P_4$ 到 $BC$ 的距离大于等于 $P_1$ 到 $BC$ 的距离，联结 $P_{1} P_{4} $ 及 $ P_{4} P_{3}$．过 $P_1$ 作平行于 $BC$ 的直线段，分别交 $P_{4} P_{3}, A C$ 于 $Q$ 及 $S$ 两点．对于同底三角形 $\triangle P_{4} P_{1} P_{2}, \triangle Q P_{1} P_{2},\triangle P_{3} P_{1} P_{2}$，我们有 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \triangle Q P_{1} P_{2} \leqslant \triangle S P_{1} P_{2}$ 由于 $\triangle P_{2} S P_{1} $ 与 $ \triangle B S P_{1}$ 同底等高，故得 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \triangle B S P_{1}$ 把 $\triangle B S P_{1}$ 放在 $\triangle B S A$ 中考察，若设 $B P_{1} : B A=x$，那么 $\triangle B S P_{1}=x \triangle B S A$ 再把 $\triangle B S A$ 放在 $\triangle ABC$ 中来看，由于 $A S : A C=1-x$，所以 $\triangle B S P_{1}=x \triangle B S A=x(1-x) \triangle A B C$ 当 $0<x<1$ 时，$x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}$，所以有 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \frac{1}{4} \triangle A B C$ 再来讨论第一幅图所示情形，联结 $P_{2} P_{3}$，利用前面已证过的情形，四个小三角形中必有一个小于等于 $\frac{1}{4} \triangle A P_{2} P_{3}$，但因 $\triangle A P_{2} P_{3}<\triangle ABC$，结论仍然正确，在竞赛中，不少同学恰恰是忽略了这一种情况．
要考虑两种情况：
（1）$\triangle ABC$ 中，有一边上不含 $P_{1}, P_{2}, P_{3}, P_{4}$ 中的任何一点，如图所示；
（2）$\triangle ABC$ 的每一条边上均有 $P_{1}, P_{2}, P_{3}, P_{4}$ 中的点，当然至少有一条边，例如 $BC$ 边上，含有其中的两个点，如图所示．先讨论后一种情形．设 $P_4$ 到 $BC$ 的距离大于等于 $P_1$ 到 $BC$ 的距离，联结 $P_{1} P_{4} $ 及 $ P_{4} P_{3}$．过 $P_1$ 作平行于 $BC$ 的直线段，分别交 $P_{4} P_{3}, A C$ 于 $Q$ 及 $S$ 两点．对于同底三角形 $\triangle P_{4} P_{1} P_{2}, \triangle Q P_{1} P_{2},\triangle P_{3} P_{1} P_{2}$，我们有 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \triangle Q P_{1} P_{2} \leqslant \triangle S P_{1} P_{2}$ 由于 $\triangle P_{2} S P_{1} $ 与 $ \triangle B S P_{1}$ 同底等高，故得 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \triangle B S P_{1}$ 把 $\triangle B S P_{1}$ 放在 $\triangle B S A$ 中考察，若设 $B P_{1} : B A=x$，那么 $\triangle B S P_{1}=x \triangle B S A$ 再把 $\triangle B S A$ 放在 $\triangle ABC$ 中来看，由于 $A S : A C=1-x$，所以 $\triangle B S P_{1}=x \triangle B S A=x(1-x) \triangle A B C$ 当 $0<x<1$ 时，$x(1-x) \leqslant\left(\frac{x+(1-x)}{2}\right)^{2}=\frac{1}{4}$，所以有 $\min \left(\triangle P_{4} P_{1} P_{2}, \triangle P_{3} P_{1} P_{2}\right) \leqslant \frac{1}{4} \triangle A B C$ 再来讨论第一幅图所示情形，联结 $P_{2} P_{3}$，利用前面已证过的情形，四个小三角形中必有一个小于等于 $\frac{1}{4} \triangle A P_{2} P_{3}$，但因 $\triangle A P_{2} P_{3}<\triangle ABC$，结论仍然正确，在竞赛中，不少同学恰恰是忽略了这一种情况．
答案
解析
备注
