1986第1届CMO试题

• 知识点

  >

  二试组合部分

略

这个题目来自罗马尼亚的一本《组合与图论问题集》．在解这个问题的时候，许多同学都画了一个边长为 $1$ 的正六边形，因为其中含有六个边长为 $1$ 的正三角形以及两个边长为 $\sqrt{3}$ 的正三角形（用虚线表示），用 $\cdot$ 与 $*$ 来表示两种不同的颜色，得出图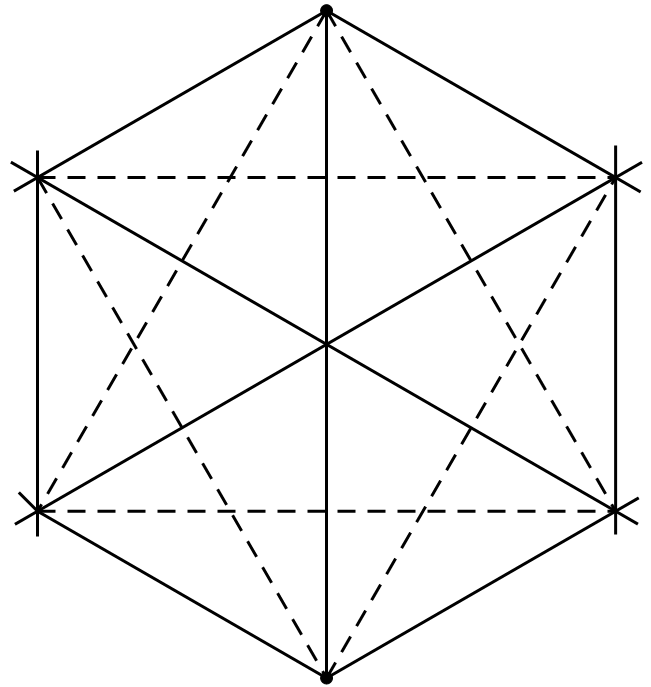但是，所有这些正三角形，三个顶点的颜色是不同的，有的同学做到这里，感到无法再进行下去，只好不了了之，半途而废．
如果能看出，上述图形不能成功的一个主要原因是：任何距离为 $2$ 的两点都是同色的．这就找到了症结之所在．
现在，设有两点 $A,B$，使 $\overline{A B}=2$，而且 $A,B$ 异色．如图所示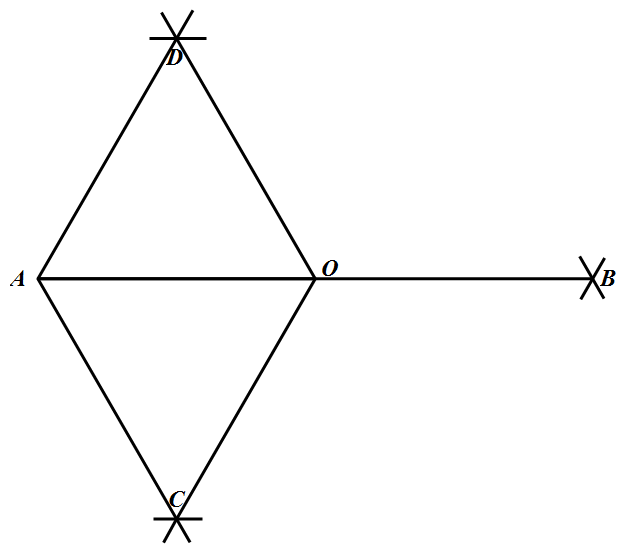取 $A$ 与 $B$ 连线的中点为 $O$，它一定与 $A$ 或 $B$ 同色．无妨设 $A,O$ 同色，以 $AO$ 为一边作两个正三角形，其他二顶点分别以 $C,D$ 记之．若 $C$ 与 $D$ 中有一个与 $A$ 同色，那么 $\triangle OAC$ 与 $\triangle OAD$ 都是边长为 $1$ 的正三角形，而且其中有一个三角形三顶点同色，结论就证明了．因此，可设 $C$ 与 $D$ 所染颜色与 $A$ 所染颜色不同，很明显，此时 $\triangle BCD$ 为一边长等于 $\sqrt{3}$ 的正三角形，三顶点同色，命题得证．
假如任何距离为 $2$ 的两点都染了相同的颜色．现在，如图所示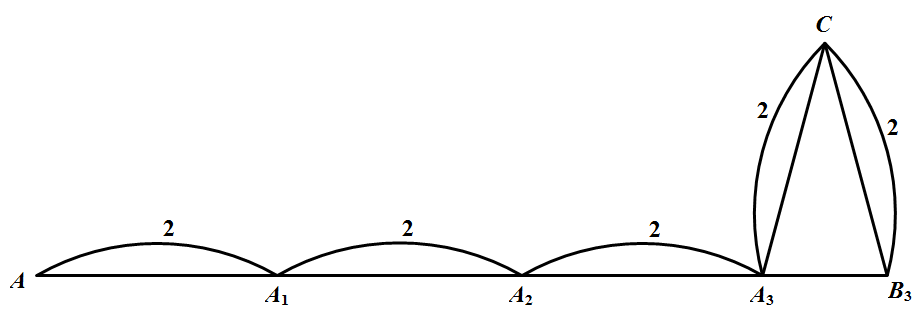任取平面上的两点 $A, B(A \neq B)$，用直线把 $A,B$ 联结起来，从 $A$ 出发，用步长 $2$ 朝 $B$ 前进，依次得到点 $A_{1}, A_{2}, A_{3}, \cdots,$ 它们与 $A$ 同色．很明显，总可以找到一点 $A_k$，使 $\overline{A_{k} B} \leqslant 2$，这时，以 $A_{k} B$ 为底边作一腰长为 $2$ 的等腰 $\triangle A_{k} C B$，依假设，这时 $C$ 与 $A_k$ 同色，$B$ 与 $C$ 同色，即 $B$ 与 $A$ 同色．这就证明了：在任何距离等于 $2$ 的两点都同色的情形下，平面上任何二点有相同的染色，即每一点只被同一种颜色所染．这时，任何边长为 $1$ 的正三角形的三顶点是同色的，结论也正确．
带有组合性质的题目都有这样的特征，必须无遗漏的考察各种可能的情况，在每一种情况下都要去证明结论的正确性．