1987第2届CMO试题

• 知识点

  >

  二试几何部分

略

以 $\alpha_{1}, \alpha_{2}, \alpha_{3}$ 记所作的三个正三角形，其面积记为 $S_{1},S_{2}, S_{3}$．因为所放五点均在原三角形（记为 $\triangle A B C$）的内部，故可以 $\triangle A B C$ 的中心为中心，在 $\triangle A B C$ 的内部作它的位似三角形 $\triangle A^{\prime} B^{\prime} C^{\prime}$，使得所放五点仍在 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 内部．$\triangle A^{\prime} B^{\prime} C^{\prime}$ 可认为是 $\triangle A B C$ 收缩而成．$\triangle A^{\prime} B^{\prime} C^{\prime}$ 面积为 $S, S=1-e, 0<e<1$．
把 $\Delta A^{\prime} B^{\prime} C^{\prime}$ 三边五等分，第 $1,4$ 分点依次为 $D_{1}, D_{2}, E_{1}, E_{2},F_{1}, F_{2}$，如图所示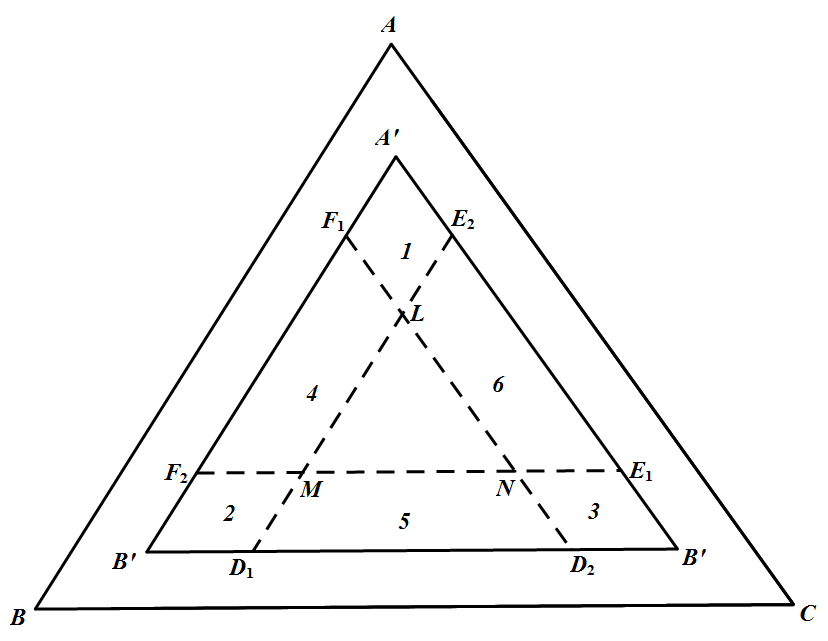联结 $D_{1} E_{2}, E_{1} F_{2}, F_{1} D_{2}$，交于 $L, M, N$，分 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 为七部分，记为小三角形 $\pi_{0}$，菱形 $\pi_{1}, \pi_{2}, \pi_{3}$，梯形 $\pi_{4}, \pi_{5}, \pi_{6}$．
（1）若有一菱形（如为 $\pi_{1}$）没放进点，则 $\pi_{2} \bigcup \pi_{4}$ 与 $\pi_{3} \bigcup \pi_{6}$ 中必有一区域（如为 $\pi_{2} \bigcup \pi_{4}$）最多放进两点，显然可作 $\alpha_{1}, \alpha_{2}$ 盖住这至多两个点，且其面积可适当任意选取，不妨设 $S_{1}=S_{2}=\delta=\dfrac{1}{2}\left(\dfrac{4}{5}\right)^{2} \varepsilon$ 令 $\alpha_3$ 为 $\triangle C^{\prime} E_{2} D_{1}$，则 $S_{3}=\left(\frac{4}{5}\right)^{2} S$，从而 $\alpha_{1}, \alpha_{2}, \alpha_{3}$ 满足要求（即盖住了五点，且三个正三角形的各边分别平行于原三角形的边），且 $S_{1}+S_{2}+S_{3}=\left(\dfrac{4}{5}\right)^{2} \varepsilon+\left(\dfrac{4}{5}\right)^{2} S=\left(\dfrac{4}{5}\right)^{2}=0.64$
（2）若每一菱形均放进点，而其余区域均没放进点，令 $\triangle A^{\prime} B^{\prime} C^{\prime}$ 各边的第 $2,3$ 分点依次为 $L_{1}, M_{2}, M_{1}, N_{2}, N_{1}, L_{2}$，如图所示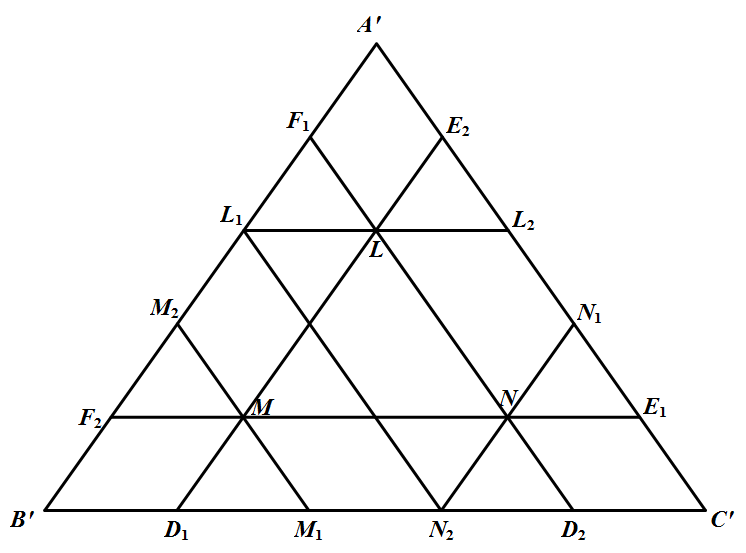则 $\Delta A^{\prime} L_{1} L_{2}, \triangle B^{\prime} M_{1} M_{2}, \triangle C^{\prime} N_{1} N_{2}$ 可作为 $\alpha_{2}, \alpha_{3}$，显然满足要求，且 $S_{1}+S_{2}+S_{3}=3\left(\dfrac{2}{5}\right)^{2} S<\left(\dfrac{4}{5}\right)^{2} S<\left(\dfrac{4}{5}\right)^{2}=0.64$
（3）若每一菱形均放进点，而其余区域只放进一点 $P$，则不妨设 $\pi_{1}$ 中放进 $2$ 点，$\pi_{2}, \pi_{3}$ 中各放进一点．
（i）$P$ 落入 $\pi_{4} \cup \pi_{0} \cup \pi_{6}$ 中，则以 $\triangle A^{\prime} F_{2} E_{1}$ 为 $\alpha_3$，情况类似于（1），同理得证；
（ii）$P$ 落入 $\pi_5$ 中，不妨设落入 $\pi_5$ 的左半部．设 $MN$ 的中点为 $Q$，过 $Q$ 作 $AC$ 的平行线，交 $B^{\prime} C^{\prime}$ 于 $N_{2}$，交 $A^{\prime} B^{\prime}$ 于 $L_{1}$．显然可作 $\alpha_{1}$ 盖住 $\pi_{3}$ 中的一点，使 $S_{1}=\delta=\left(\frac{1}{5}\right)^{2} S$；令 $\alpha_{2}$ 为 $\triangle A^{\prime} L_{1} L_{2}, \alpha_{3}$ 为 $\triangle B^{\prime} N_{2} F$，则 $\alpha_{2}$ 盖住 $\pi_{1}$ 中的两点，$\alpha_3$ 盖住了 $\pi_{2}$ 中的一点和点 $P$，$\alpha_{1}, \alpha_{2}, \alpha_{3}$ 符合要求，且 $\begin{aligned} S_{1}+S_{2}+S_{3}=&\left(\left(\frac{1}{5}\right)^{2}+\left(\frac{2}{5}\right)^{2}+\left(\frac{3}{5}\right)^{2}\right) S< \left(\frac{4}{5}\right)^{2} S<\left(\frac{4}{5}\right)^{2}=0.64 \end{aligned}$
（4）若每一菱形均放进点，而其余区域也放进两点 $P,Q$，则 $\pi_{1}, \pi_{2}, \pi_{3}$ 中各放进一点，而三个梯形中至少有一（如为 $\pi_4$）没放进点，则以 $\triangle C^{\prime} D_{1} E_{2}$ 为 $\alpha_{3}$，情况类似于（1），同理得证，证毕．