设 $A_{1} A_{2} A_{3} A_{4}$ 是一个四面体，$S_{1}, S_{2}, S_{3}, S_{4}$ 分别是以 $A_1,A_{2}, A_{3}, A_{4}$ 为球心的球，它们两两相切．如果存在一点 $Q$，以这点为球心可作一个半径为 $r$ 的球与 $S_{1}, S_{2}, S_{3}, S_{4}$ 都想切，还可以作一个半径为 $R$ 的球与四面体的各棱都相切．求证：这个四面体是正四面体．
【难度】
【出处】
1987第2届CMO试题
【标注】
【答案】
略
【解析】
先证明一条引理
引理：设有 $\triangle A_{1} A_{2} A_{3}, S_{1}, S_{2}, S_{3}$ 分别是以 $A_{1}, A_{2}, A_{3}$ 为圆心的圆，它们两两相切．如果存在一点 $O$，以这点为圆心可作一个半径为 $r$ 的圆与 $S_{1}, S_{2}, S_{3}$ 都相切，还可作一个半径为 $R$ 的圆与 $\triangle A_{1} A_{2} A_{3}$ 的各边都相切，则 $\triangle A_{1} A_{2} A_{3}$ 为正三角形．
引理的证明（1）先设 $S_{1}, S_{2}, S_{3}$ 两两外切．
（i）若圆 $O(r)$ 与 $S_{1}, S_{2}, S_{3}$ 均外切．如图所示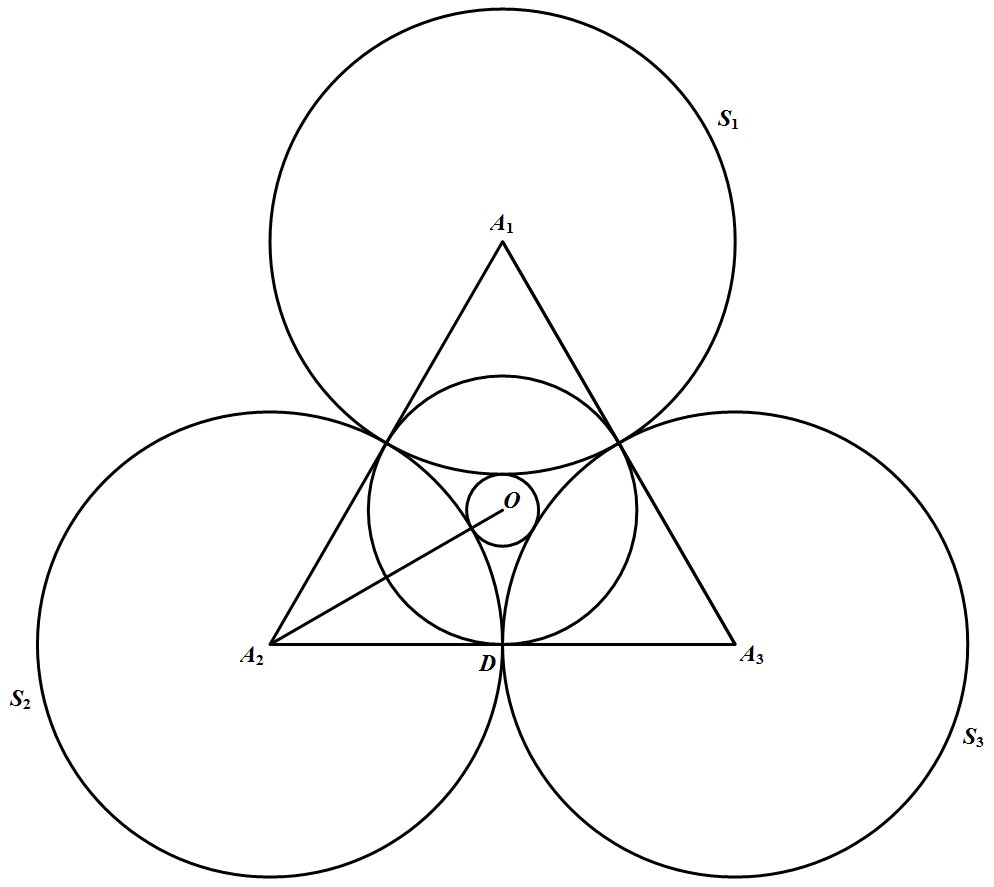
设圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的内切圆，与 $A_{2} A_{3}$ 切于 $D$．令圆 $S_{1}, S_{2}, S_{3}$ 的半径分别为 $r_{1}, r_{2}, r_{3}$．若 $r\left(r+2 r_{2}\right)>R^{2}$，则 $A_{2} D=\sqrt{\left(r+r_{2}\right)^{2}-R^{2}}>r_{2}$ 从而 $A_{3} D<r_{2}$，推出 $r\left(r+2 r_{3}\right)<R^{2}$；同理，由 $r\left(r+2 r_{3}\right)<R^{2}$ 可推得 $r\left(r+2 r_{1}\right)>R^{2}$，又可推得 $r\left(r+2 r_{2}\right)<R^{2}$，引出矛盾．同理设 $r\left(r+2 r_{2}\right)<R^{2}$ 也推出矛盾，所以 $r\left(r+2 r_{2}\right)=R^{2}$，同理 $r\left(r+2 r_{1}\right)=r\left(r+2 r_{2}\right)=r\left(r+2 r_{3}\right)=R^{2}$ 推得 $r_{1}=r_{2}=r_{3}$，若记 $a, b, c$ 为 $\triangle A_{1} A_{2} A_{3}$ 的三边，则有 $a=b
=c,\triangle A_{1} A_{2} A_{3}$ 为正三角形．
（ii）若圆 $O(R)$ 与 $S_{1}, S_{2}, S_{3}$ 均内切，类似于（i），只须把 $r+2 r_{1}, r,+2 r_{2}, r+2 r_{3}$ 相应的改为 $r-2 r_{1}, r-2 r_{2}, r-2 r_{3}$ 即可，仍可证得 $\triangle A_{1} A_{2} A_{3}$ 为正三角形）（不考虑圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的旁切圆的情形）．
（2）再设 $S_{1}, S_{2}, S_{3}$ 中有一对外切，两对内切，则易证得点 $O$ 必在 $\triangle A_{1} A_{2} A_{3}$ 外，不可能作圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的内切圆．易知 $S_{1}, S_{2}, S_{3}$ 不可能再有 其他情形，证毕．
下面证明原题．
（1）先设 $S_{1}, S_{2}, S_{3}, S_{4}$ 两两外切．用完全类似于引理证明中的（1）的方法，可推得：对于 $\triangle A_{1} A_{2} A_{3}$，有 $A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{1}$，$\triangle A_{1} A_{2} A_{3}$ 为正三角形；．．．；$\triangle A_{2} A_{3} A_{4}$ 为正三角形（亦即应用"圆幂定理"的推广"球幂定理"）．从而得四面体 $A_{1} A_{2} A_{3} A_{4}$ 为正四面体．
（2）再设 $S_{1}, S_{2}, S_{3}, S_{4}$ 不两两外切，用类似于引理证明中的（2）的方法，也易知不可能作球 $O(R)$ 与六条棱 $A_{1} A_{2}, \cdots, A_{3} A_{4}$ 均相切．证毕．
引理：设有 $\triangle A_{1} A_{2} A_{3}, S_{1}, S_{2}, S_{3}$ 分别是以 $A_{1}, A_{2}, A_{3}$ 为圆心的圆，它们两两相切．如果存在一点 $O$，以这点为圆心可作一个半径为 $r$ 的圆与 $S_{1}, S_{2}, S_{3}$ 都相切，还可作一个半径为 $R$ 的圆与 $\triangle A_{1} A_{2} A_{3}$ 的各边都相切，则 $\triangle A_{1} A_{2} A_{3}$ 为正三角形．
引理的证明（1）先设 $S_{1}, S_{2}, S_{3}$ 两两外切．
（i）若圆 $O(r)$ 与 $S_{1}, S_{2}, S_{3}$ 均外切．如图所示
设圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的内切圆，与 $A_{2} A_{3}$ 切于 $D$．令圆 $S_{1}, S_{2}, S_{3}$ 的半径分别为 $r_{1}, r_{2}, r_{3}$．若 $r\left(r+2 r_{2}\right)>R^{2}$，则 $A_{2} D=\sqrt{\left(r+r_{2}\right)^{2}-R^{2}}>r_{2}$ 从而 $A_{3} D<r_{2}$，推出 $r\left(r+2 r_{3}\right)<R^{2}$；同理，由 $r\left(r+2 r_{3}\right)<R^{2}$ 可推得 $r\left(r+2 r_{1}\right)>R^{2}$，又可推得 $r\left(r+2 r_{2}\right)<R^{2}$，引出矛盾．同理设 $r\left(r+2 r_{2}\right)<R^{2}$ 也推出矛盾，所以 $r\left(r+2 r_{2}\right)=R^{2}$，同理 $r\left(r+2 r_{1}\right)=r\left(r+2 r_{2}\right)=r\left(r+2 r_{3}\right)=R^{2}$ 推得 $r_{1}=r_{2}=r_{3}$，若记 $a, b, c$ 为 $\triangle A_{1} A_{2} A_{3}$ 的三边，则有 $a=b=c,\triangle A_{1} A_{2} A_{3}$ 为正三角形．
（ii）若圆 $O(R)$ 与 $S_{1}, S_{2}, S_{3}$ 均内切，类似于（i），只须把 $r+2 r_{1}, r,+2 r_{2}, r+2 r_{3}$ 相应的改为 $r-2 r_{1}, r-2 r_{2}, r-2 r_{3}$ 即可，仍可证得 $\triangle A_{1} A_{2} A_{3}$ 为正三角形）（不考虑圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的旁切圆的情形）．
（2）再设 $S_{1}, S_{2}, S_{3}$ 中有一对外切，两对内切，则易证得点 $O$ 必在 $\triangle A_{1} A_{2} A_{3}$ 外，不可能作圆 $O(R)$ 为 $\triangle A_{1} A_{2} A_{3}$ 的内切圆．易知 $S_{1}, S_{2}, S_{3}$ 不可能再有 其他情形，证毕．
下面证明原题．
（1）先设 $S_{1}, S_{2}, S_{3}, S_{4}$ 两两外切．用完全类似于引理证明中的（1）的方法，可推得：对于 $\triangle A_{1} A_{2} A_{3}$，有 $A_{1} A_{2}=A_{2} A_{3}=A_{3} A_{1}$，$\triangle A_{1} A_{2} A_{3}$ 为正三角形；．．．；$\triangle A_{2} A_{3} A_{4}$ 为正三角形（亦即应用"圆幂定理"的推广"球幂定理"）．从而得四面体 $A_{1} A_{2} A_{3} A_{4}$ 为正四面体．
（2）再设 $S_{1}, S_{2}, S_{3}, S_{4}$ 不两两外切，用类似于引理证明中的（2）的方法，也易知不可能作球 $O(R)$ 与六条棱 $A_{1} A_{2}, \cdots, A_{3} A_{4}$ 均相切．证毕．
答案
解析
备注
