$m$ 个互不相同的正偶数与 $n$ 个互不相同的正奇数的总和为 $1987$，对于所有这样的 $m$ 与 $n$，问 $3m+4n$ 的最大值是多少？请证明你的结论．
【难度】
【出处】
1987第2届CMO试题
【标注】
【答案】
略
【解析】
欲使 $s=3 m+4 n$ 尽可能大，须使作出 $m$ 个偶数 $a_{1}, \cdots,a_m$ 和 $n$ 个奇数 $b_{1}, \cdots, b_{n}$ 尽可能小，因此考虑不等式 $(2+4+\cdots+2 m)+(1+3+\cdots+(2 n-1)) \leqslant 1987 $ ①
式 ① 即 $m(m+1)+n^{2} \leqslant 1987$ ②
式 ② 表示 $mn$ 平面上的圆盘 $\left(m+\frac{1}{2}\right)^{2}+n^{2} \leqslant \frac{7949}{4}$ ③
所有合条件的数对 $(m,n)$，以此为坐标的点均落入圆盘 ③ 与第一象限（包括坐标轴）的公共范围，如图所示．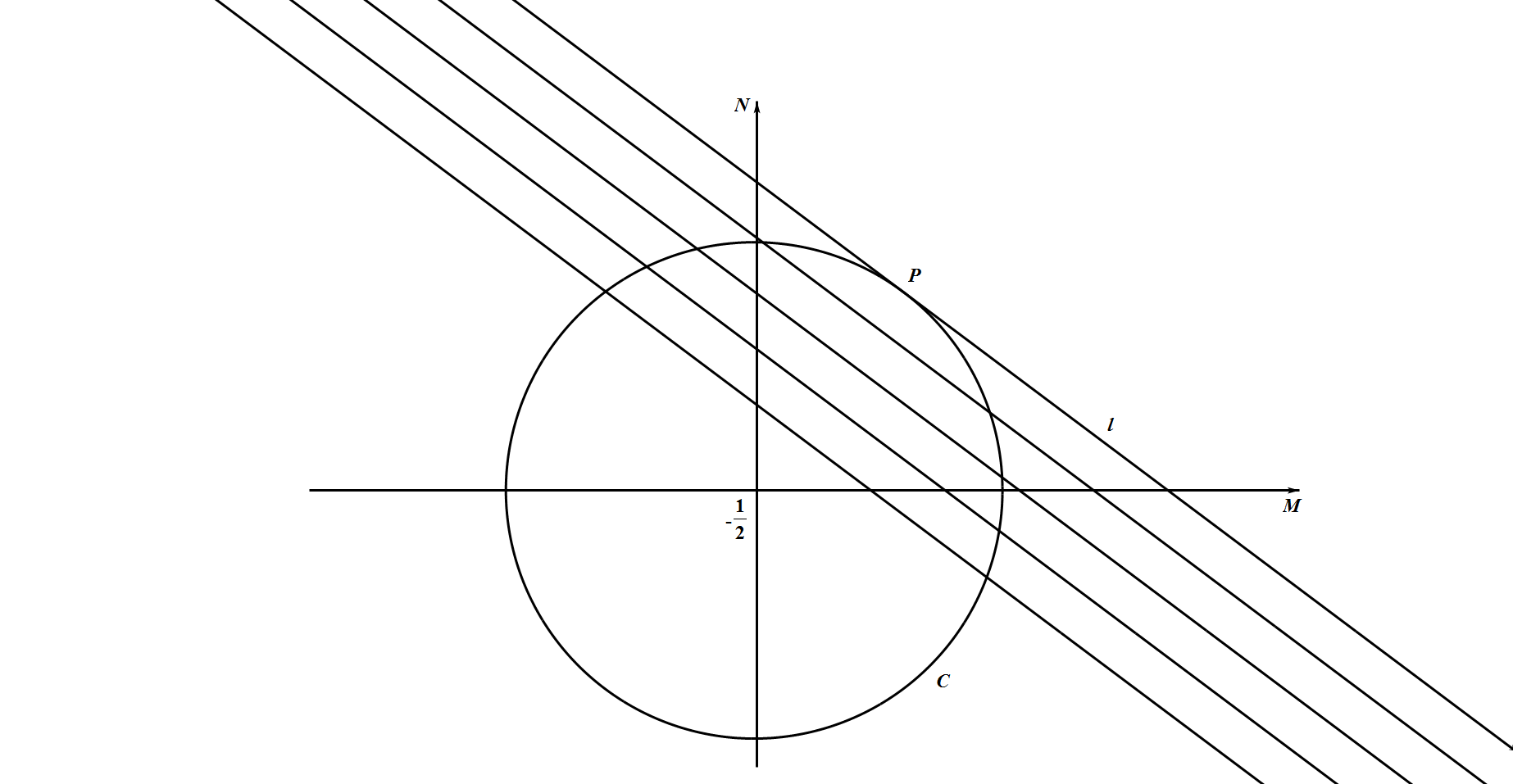
作一组平行直线：$3m+4n=s$（$s$ 为正整数），所求 $3m+4n$ 的最大值应为使得直线 $3m+4n=s$ 与圆盘 ③ 有为整点的交点的 $s$ 的最大值．
如不限制 $s$ 为正整数，则使得平行直线组 $3m+4n=s$ 与圆盘 ③ 有交点的 $s$ 的最大值，出现在 $3m+4n=s$ 为圆盘 ③ 的切线 $l$ 的情况下，这时切点 $P(m,n)$ 满足 $-\frac{3}{4}=-\frac{m+\frac{1}{2}}{n} \Rightarrow 3 n=4 m+2$ 代入 $m(m+1)+n^{2}=1987$ 解得 $m=\frac{3}{10} \sqrt{7949}-\frac{1}{2}, n=\frac{2}{5} \sqrt{7949}$ ④
$s=3 m+4 n=\frac{5}{2} \sqrt{7949}-\frac{3}{2}$ 因为 $89^{2}<7949<89.16^{2}$ 所以 $221<s<221.4$ 考虑到 $s$ 为正整数，便有 $s$ 的最大值小于等于 $221$．把直线 $l$ 平行地左移，碰到第一格点 $Q(m,n)$（在圆盘 ③ 中），则 $s=3m+4n$ 便为最大值．由于 $n$ 显然为奇数，所以应改述为"碰到第一满足 $n$ 为奇数的格点 $Q(m,n)$ "，这个格点的纵坐标 $n$ 应尽可能接近 $\dfrac{2}{5}\sqrt{7949}=35.6\cdots$，故可考虑 $n=35$ 或 $n=37$．前者使得 $m(m+1)\leqslant 1987-n^2=762$，$m$ 的最大值为 $27$，$s$ 的最大值为 $221$；后者可同样计算得 $s$ 的最大值为 $220$，故应取前者．实际构造可取（并非唯一）$\begin{aligned} a_{1}=& 2, a_{2}=4, \cdots, a_{26}=52, a_{27}=60 , m=27, b_{1} =1, b_{2}=3, \cdots, b_{35}=69 , n =35 \end{aligned}$ 则得
$a_{1}+a_{2}+\cdots+a_{27}+b_{1}+\cdots+b_{35}=1987$ 同理 $s=3 m+4 n=221$ 取最大值．
式 ① 即 $m(m+1)+n^{2} \leqslant 1987$ ②
式 ② 表示 $mn$ 平面上的圆盘 $\left(m+\frac{1}{2}\right)^{2}+n^{2} \leqslant \frac{7949}{4}$ ③
所有合条件的数对 $(m,n)$，以此为坐标的点均落入圆盘 ③ 与第一象限（包括坐标轴）的公共范围，如图所示．
作一组平行直线：$3m+4n=s$（$s$ 为正整数），所求 $3m+4n$ 的最大值应为使得直线 $3m+4n=s$ 与圆盘 ③ 有为整点的交点的 $s$ 的最大值．如不限制 $s$ 为正整数，则使得平行直线组 $3m+4n=s$ 与圆盘 ③ 有交点的 $s$ 的最大值，出现在 $3m+4n=s$ 为圆盘 ③ 的切线 $l$ 的情况下，这时切点 $P(m,n)$ 满足 $-\frac{3}{4}=-\frac{m+\frac{1}{2}}{n} \Rightarrow 3 n=4 m+2$ 代入 $m(m+1)+n^{2}=1987$ 解得 $m=\frac{3}{10} \sqrt{7949}-\frac{1}{2}, n=\frac{2}{5} \sqrt{7949}$ ④
$s=3 m+4 n=\frac{5}{2} \sqrt{7949}-\frac{3}{2}$ 因为 $89^{2}<7949<89.16^{2}$ 所以 $221<s<221.4$ 考虑到 $s$ 为正整数，便有 $s$ 的最大值小于等于 $221$．把直线 $l$ 平行地左移，碰到第一格点 $Q(m,n)$（在圆盘 ③ 中），则 $s=3m+4n$ 便为最大值．由于 $n$ 显然为奇数，所以应改述为"碰到第一满足 $n$ 为奇数的格点 $Q(m,n)$ "，这个格点的纵坐标 $n$ 应尽可能接近 $\dfrac{2}{5}\sqrt{7949}=35.6\cdots$，故可考虑 $n=35$ 或 $n=37$．前者使得 $m(m+1)\leqslant 1987-n^2=762$，$m$ 的最大值为 $27$，$s$ 的最大值为 $221$；后者可同样计算得 $s$ 的最大值为 $220$，故应取前者．实际构造可取（并非唯一）$\begin{aligned} a_{1}=& 2, a_{2}=4, \cdots, a_{26}=52, a_{27}=60 , m=27, b_{1} =1, b_{2}=3, \cdots, b_{35}=69 , n =35 \end{aligned}$ 则得
$a_{1}+a_{2}+\cdots+a_{27}+b_{1}+\cdots+b_{35}=1987$ 同理 $s=3 m+4 n=221$ 取最大值．
答案
解析
备注
