设 $C_1,C_2$ 是同心圆，$C_2$ 的半径是 $C_1$ 半径的 $2$ 倍．四边形 $A_1A_2A_3A_4$ 内接于 $C_1$，将 $A_4A_1$ 延长交圆 $C_2$ 于 $B_1$，$A_1A_2$ 延长交圆 $C_2$ 于 $B_2$，$A_2A_3$ 延长交圆 $C_2$ 与 $B_3$，$A_3A_4$ 延长交圆 $C_2$ 与 $B_4$．试证：四边形 $B_{1} B_{2} B_{3} B_{4}$ 的周长大于等于 $2\times$ 四边形 $A_{1} A_{2} A_{3} A_{4}$ 的周长．并请确定等号成立的条件．
【难度】
【出处】
1988第3届CMO试题
【标注】
【答案】
略
【解析】
如图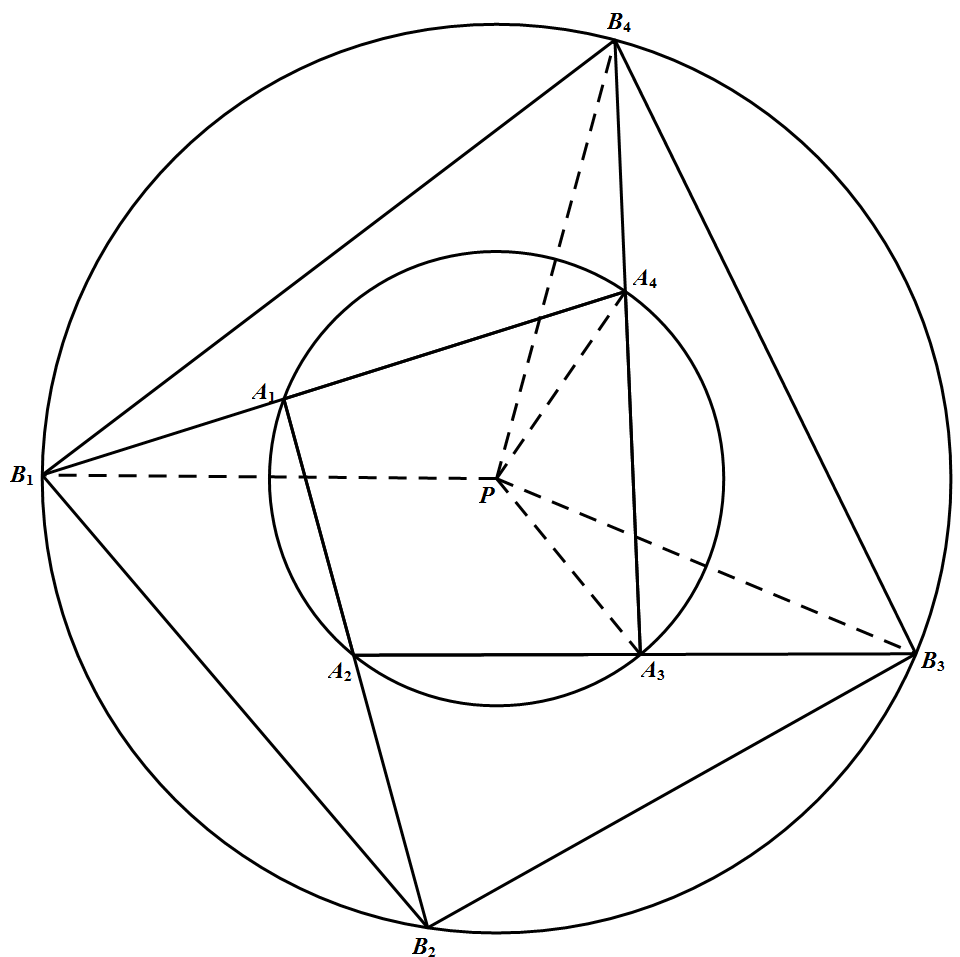
记两同心圆的圆心为 $P$，联结 $P A_{3}$ 及 $P A_{4}$，由托勒密定理 ${P B_{3}} \cdot {A_{3} B_{4}} \leqslant {P A_{3}} \cdot {B_{3} B_{4}}+{A_{3} B_{3}} \cdot {P B_{4}}$ 因为 $P B_{4}=2 P A_{3}, A_{3} B_{4}=A_{3} A_{4}+A_{4} B_{4}$ 所以 $2\left({A_{3} A_{4}}+{A_{4} B_{4}}\right) \leqslant {B_{3} B_{4}}+2 {A_{3} B_{3}}$ ① 类似地可得另三个不等式（把下标 $3,4$ 换成 $4,1$；$1,2$ 及 $2,3$）．这四个不等式相加，即得 $2\left({A_{1} A_{2}}+{A_{2} A_{3}}+{A_{3} A_{4}}+{A_{4} A_{1}}\right) \leqslant {B_{1} B_{2}}+{B_{2} B_{3}}+{B_{3} B_{4}}+{B_{4} B_{1}}$ 要使不等式 ① 及类似的另三个不等式都成为等式，由托勒密定理，式 ① 成立等式的充分必要条件是 $P, A_{3}, B_{3}, B_{4}$ 这四点共圆，从而 $\angle P A_{3} A_{2}=\angle P B_{4} B_{3}=\angle P B_{3} B_{4}=\angle P A_{3} B_{4}$，所以 ${A_{2} A_{3}}={A_{3} A_{4}}$．同理，$P, A_{4}, B_{4}, B_{1}$ 四点共圆可得 ${A_{4} A_{3}}={A_{4} A_{1}}$，以及 ${A_{1} A_{2}}={A_{2} A_{3}}$．所以 $A_{1} A_{2} A_{3} A_{4}$ 是正方形．
反之，如果 $A_{1} A_{2} A_{3} A_{4}$ 是正方形，$\angle P A_{3} A_{2}=\angle P A_{3} A_{4}$，用同一法既知 $P, A_{3}, B_{3}, B_{4}$ 共圆．从而式 ① 成为等式．同理，另三个也成为等式，从而 ${B_{1} B_{2}}+{B_{2} B_{3}}+{B_{3} B_{4}}+{B_{4} B_{1}}=2\left({A_{1} A_{2}}+{A_{2} A_{3}}+{A_{3} A_{4}}+{A_{4} A_{1}}\right)$
记两同心圆的圆心为 $P$，联结 $P A_{3}$ 及 $P A_{4}$，由托勒密定理 ${P B_{3}} \cdot {A_{3} B_{4}} \leqslant {P A_{3}} \cdot {B_{3} B_{4}}+{A_{3} B_{3}} \cdot {P B_{4}}$ 因为 $P B_{4}=2 P A_{3}, A_{3} B_{4}=A_{3} A_{4}+A_{4} B_{4}$ 所以 $2\left({A_{3} A_{4}}+{A_{4} B_{4}}\right) \leqslant {B_{3} B_{4}}+2 {A_{3} B_{3}}$ ① 类似地可得另三个不等式（把下标 $3,4$ 换成 $4,1$；$1,2$ 及 $2,3$）．这四个不等式相加，即得 $2\left({A_{1} A_{2}}+{A_{2} A_{3}}+{A_{3} A_{4}}+{A_{4} A_{1}}\right) \leqslant {B_{1} B_{2}}+{B_{2} B_{3}}+{B_{3} B_{4}}+{B_{4} B_{1}}$ 要使不等式 ① 及类似的另三个不等式都成为等式，由托勒密定理，式 ① 成立等式的充分必要条件是 $P, A_{3}, B_{3}, B_{4}$ 这四点共圆，从而 $\angle P A_{3} A_{2}=\angle P B_{4} B_{3}=\angle P B_{3} B_{4}=\angle P A_{3} B_{4}$，所以 ${A_{2} A_{3}}={A_{3} A_{4}}$．同理，$P, A_{4}, B_{4}, B_{1}$ 四点共圆可得 ${A_{4} A_{3}}={A_{4} A_{1}}$，以及 ${A_{1} A_{2}}={A_{2} A_{3}}$．所以 $A_{1} A_{2} A_{3} A_{4}$ 是正方形．反之，如果 $A_{1} A_{2} A_{3} A_{4}$ 是正方形，$\angle P A_{3} A_{2}=\angle P A_{3} A_{4}$，用同一法既知 $P, A_{3}, B_{3}, B_{4}$ 共圆．从而式 ① 成为等式．同理，另三个也成为等式，从而 ${B_{1} B_{2}}+{B_{2} B_{3}}+{B_{3} B_{4}}+{B_{4} B_{1}}=2\left({A_{1} A_{2}}+{A_{2} A_{3}}+{A_{3} A_{4}}+{A_{4} A_{1}}\right)$
答案
解析
备注
